
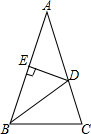
 如圖,在△ABC中,AB=AC,∠A=36°,BD為角平分線,DE⊥AB,垂足為E.
如圖,在△ABC中,AB=AC,∠A=36°,BD為角平分線,DE⊥AB,垂足為E.分析 (1)利用等腰三角形的性質和三角形的內角和可求出圖中所有角的度數,從而可得到△ADE≌△BDE,△ABC∽△BCD;
(2)利用有兩組角對應相等的兩個三角形相似可證明△ABC∽△BCD;
(3)先證明AD=BD=BC,再利用△ABC∽△BCD得到$\frac{AC}{BC}$=$\frac{BC}{CD}$,則AC•(AC-AD)=AD2,然后解關于AC的一元二次方程即可得到AD:AC的值.
解答 解:(1)△ADE≌△BDE,△ABC∽△BCD;
(2)∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-36°)=72°,
∵BD為角平分線,
∴∠CBD=∠ABD=$\frac{1}{2}$∠ABC=36°,
∴∠CBD=∠A,
而∠BCD=∠ACB,
∴△ABC∽△BCD;
(3)∵∠A=∠ABD=36°,
∴AD=BD,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,
∵△ABC∽△BCD,
∴$\frac{AC}{BC}$=$\frac{BC}{CD}$,
即AC•(AC-AD)=AD2,
整理得AD2+AC•AD-AC2=0,
解得AD=$\frac{-1+\sqrt{5}}{2}$AC或AD=$\frac{-1-\sqrt{5}}{2}$AC(舍去),
∴AD:AC的值為$\frac{\sqrt{5}-1}{2}$.
點評 本題考查了相似三角形的判定:有兩組角對應相等的兩個三角形相似.也考查了相似三角形的性質和等腰三角形的性質.


 學習實踐園地系列答案
學習實踐園地系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖是一個橫斷面為拋物線形狀的拱橋,當水面寬4米時,拱頂(拱橋洞的最高點)離水面2米,水面上升1米時,水面的寬度為2$\sqrt{2}$米.
如圖是一個橫斷面為拋物線形狀的拱橋,當水面寬4米時,拱頂(拱橋洞的最高點)離水面2米,水面上升1米時,水面的寬度為2$\sqrt{2}$米.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com