
 如圖,已知直線l1∥l2,且l3和l1,l2分別交于A,B兩點,點P在直線l3上,且不和點A,B重合.
如圖,已知直線l1∥l2,且l3和l1,l2分別交于A,B兩點,點P在直線l3上,且不和點A,B重合.分析 (1)過點P作l1的平行線,根據平行線的性質進行解題;
(2)當點P在下側時,過點P作l1的平行線PQ,由平行線的性質可得出l1∥l2∥PQ,由此即可得出結論.
解答 解:(1)∠1+∠2=∠3;
理由:如圖1,過點P作l1的平行線,
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠1=∠4,∠2=∠5,
∵∠4+∠5=∠3,
∴∠1+∠2=∠3;
(2)∠1-∠2=∠3或∠2-∠1=∠3.
理由:如圖2,當點P在下側時,過點P作l1的平行線PQ,
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠2=∠4,∠1=∠3+∠4,
∴∠1-∠2=∠3;
當點P在上側時,同理可得∠2-∠1=∠3.
點評 本題考查的是平行線的性質,根據題意作出輔助線是解答此題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
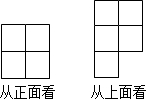 用若干大小相同的小正方塊搭一個幾何體,使得從正面和從上面看到的這個幾何體的形狀如圖所示,那么搭這樣一個幾何體最少需要多少個小正方塊( )
用若干大小相同的小正方塊搭一個幾何體,使得從正面和從上面看到的這個幾何體的形狀如圖所示,那么搭這樣一個幾何體最少需要多少個小正方塊( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com