
【題目】某同學所在年級的500名學生參加志愿者活動,現有以下5個志愿服務項目:A,紀念館志講解員.B.書香社區圖書整理C.學編中國結及義賣.D,家風講解員E.校內志愿服務,要求:每位學生都從中選擇一個項目參加,為了了解同學們選擇這個5個項目的情況,該同學隨機對年級中的40名同學選擇的志愿服務項目進行了調查,過程如下:
收集數據:設計調查問卷,收集到如下數據(志愿服務項目的編號,用字母代號表示)
B,E,B,A,E,C,C,C,B,B,
A,C,E,D,B,A,B,E,C,A,
D,D,B,B,C,C,A,E,B
C,B,D,C,A,C,C,A,C,E,
(1)整理、描述詩句:劃記、整理、描述樣本數據,繪制統計圖如下,請補全統計表和統計圖

選擇各志愿服務項目的人數統計表
志愿服務項目 | 劃記 | 人數 |
A.紀念館志愿講解員 | 正 | 8 |
B.書香社區圖書整理 | ||
C.學編中國結及義賣 | 正正 | 12 |
D.家風講解員 | ||
E.校內志愿服務 | 正 一 | 6 |
合計 | 40 | 40 |
分析數據、推斷結論
(2)抽樣的40個樣本數據(志愿服務項目的編號)的眾數是 (填A﹣E的字母代號)
(3)請你任選A﹣E中的兩個志愿服務項目,根據該同學的樣本數據估計全年級大約有多少名同學選擇這兩個志愿服務項目.
【答案】(1)B占25%,D占10%.(2)C(3)A:500×20%=100(人).B:500×25%=125(人).C:500×30%=150(人).D:500×10%=50(人).E:500×15%=75(人).
【解析】
依據收集的數據,即可得到補全統計表和統計圖;依據抽樣的40個樣本數據(志愿服務項目的編號)中,C出現的次數最多,可得眾數是C.依據A-E中的各志愿服務項目在樣本中所占的百分比,即可得到全年級大約有多少名同學選擇某兩個志愿服務項目.
整理、描述數據:
(1)由題可得,A項有8人,B項有10人,D項有4人.
選擇各志愿服務項目的人數比例統計圖中,B占10÷40=25%,D占4÷40=10%.
分析數據、推斷結論:
(2)抽樣的40個樣本數據(志愿服務項目的編號)中,C出現的次數最多,故眾數是C.
故答案為:C.
(3)(寫出任意兩個即可).A:500×20%=100(人).B:500×25%=125(人).C:500×30%=150(人).D:500×10%=50(人).E:500×15%=75(人).


科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點A和點B(3,0),與
軸交于點A和點B(3,0),與![]() 軸交于點C(0,3).
軸交于點C(0,3).

(1)求拋物線的解析式;
(2)若點M是拋物線在![]() 軸下方上的動點,過點M作MN//
軸下方上的動點,過點M作MN//![]() 軸交直線BC于點N,求線段MN的最大值;
軸交直線BC于點N,求線段MN的最大值;
(3)在(2)的條件下,當MN取最大值時,在拋物線的對稱軸![]() 上是否存在點P,使△PBN是等腰三角形?若存在,請直接寫出所有點P的坐標;若不存在,請說明理由.
上是否存在點P,使△PBN是等腰三角形?若存在,請直接寫出所有點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC 中,AB=AC, ∠BAC <60°,將線段 AB 繞點 A逆時針旋轉 60°得到點 D, 點 E 與點 D 關于直線 BC 對稱,連接 CD,CE,DE.
(1)依題意補全圖形;
(2)判斷△CDE 的形狀,并證明;
(3)請問在直線CE上是否存在點 P,使得 PA - PB =CD 成立?若存在,請用文字描述出點 P 的準確位置,并畫圖證明;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校初二和初三兩個年級各有600名同學,為了科普衛生防疫知識,學校組織了一次在線知識競賽,小宇分別從初二、初三兩個年級隨機抽取了40名同學的成績(百分制),并對數據(成績)進行整理、描述和分析,下面給出了部分信息.
![]() .初二、初三年級學生知識競賽成績不完整的頻數分布直方圖如下(數據分成5組:
.初二、初三年級學生知識競賽成績不完整的頻數分布直方圖如下(數據分成5組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
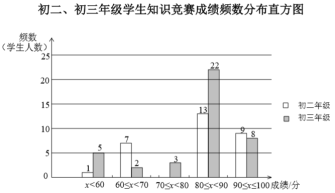
![]() .初二年級學生知識競賽成績在
.初二年級學生知識競賽成績在![]() 這一組的數據如下:
這一組的數據如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() .初二、初三學生知識競賽成績的平均數、中位數、方差如下:
.初二、初三學生知識競賽成績的平均數、中位數、方差如下:
平均數 | 中位數 | 方差 | |
初二年級 | 80.8 |
| 96.9 |
初三年級 | 80.6 | 86 | 153.3 |
根據以上信息,回答下列問題:
(1)補全上面的知識競賽成績頻數分布直方圖;
(2)寫出表中![]() 的值;
的值;
(3)![]() 同學看到上述的信息后,說自己的成績能在本年級排在前40%,
同學看到上述的信息后,說自己的成績能在本年級排在前40%,![]() 同學看到
同學看到![]() 同學的成績后說:“很遺憾,你的成績在我們年級進不了前50%”.請判斷
同學的成績后說:“很遺憾,你的成績在我們年級進不了前50%”.請判斷![]() 同學是________(填“初二”或“初三”)年級的學,你判斷的理由是________.
同學是________(填“初二”或“初三”)年級的學,你判斷的理由是________.
(4)若成績在85分及以上為優秀,請估計初二年級競賽成績優秀的人數為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了迎接2022年的冬奧會,中小學都積極開展冰上運動,小乙和小丁進行500米短道速滑比賽,他們的五次成績(單位:秒)如表所示:
1 | 2 | 3 | 4 | 5 | |
小乙 | 45 | 63 | 55 | 52 | 60 |
小丁 | 51 | 53 | 58 | 56 | 57 |
設兩人的五次成績的平均數依次為![]() 乙,
乙,![]() 丁,成績的方差一次為
丁,成績的方差一次為![]() ,
,![]() ,則下列判斷中正確的是( )
,則下列判斷中正確的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,過⊙T外一點P引它的兩條切線,切點分別為M,N,若![]() ,則稱P為⊙T的環繞點.
,則稱P為⊙T的環繞點.
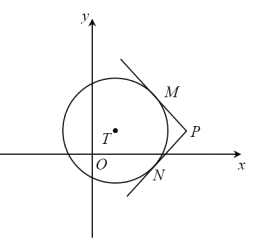
(1)當⊙O半徑為1時,
①在![]() 中,⊙O的環繞點是___________;
中,⊙O的環繞點是___________;
②直線y=2x+b與x軸交于點A,y軸交于點B,若線段AB上存在⊙O的環繞點,求b的取值范圍;
(2)⊙T的半徑為1,圓心為(0,t),以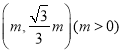 為圓心,
為圓心,![]() 為半徑的所有圓構成圖形H,若在圖形H上存在⊙T的環繞點,直接寫出t的取值范圍.
為半徑的所有圓構成圖形H,若在圖形H上存在⊙T的環繞點,直接寫出t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景:如圖,將![]() 繞點
繞點![]() 逆時針旋轉60°得到
逆時針旋轉60°得到![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,可推出結論:
,可推出結論:![]()
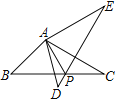
問題解決:如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .點
.點![]() 是
是![]() 內一點,則點
內一點,則點![]() 到
到![]() 三個頂點的距離和的最小值是___________
三個頂點的距離和的最小值是___________
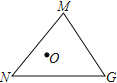
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從﹣4、3、5這三個數中,隨機抽取一個數,記為a,那么,使關于x的方程x2+4x+a=0有解,且使關于x的一次函數y=2x+a的圖象與x軸、y軸圍成的三角形面積恰好為4的概率_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】受非洲豬瘟疫情影響,2019年我國豬肉價格有較大幅度的上升.為了解某地區養殖戶的受災情況,現從該地區建檔的養殖戶中隨機抽取了部分養殖戶進行調查(把調查結果分為四個等級:A級-非常嚴重,B級-嚴重,C級-一般,D級-沒有感染),并將調查結果繪制成如下兩幅不完整的統計圖.請根據統計圖中的信息解答下列問題:
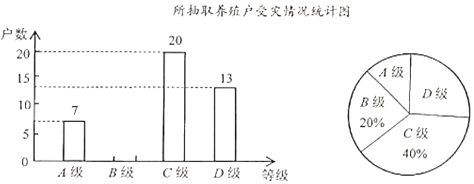
(1)填空:本次抽樣調查的養殖戶的總戶數是______;在扇形統計圖中![]() 級所對應的圓心角為______度;
級所對應的圓心角為______度;
(2)請補全條形統計圖;
(3)若該地區建檔的養殖戶有1500戶,估計非常嚴重與嚴重的養殖戶一共有多少戶?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com