
【題目】如圖(1)四邊形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,點E在CD的延長線上,∠BAC=∠DAE.
(1)求證:△ABC≌△ADE;
(2)求證:CA平分∠BCD;
(3)如圖(2),設AF是△ABC的BC邊上的高,求證:EC=2AF.

【答案】(1)詳見解析(2)詳見解析;(3)詳見解析.
【解析】
(1)根據全等三角形的判定定理ASA即可證得.
(2)通過三角形全等求得AC=AE,∠BCA=∠E,進而根據等邊對等角求得∠ACD=∠E,從而求得∠BCA=∠E=∠ACD即可證得.
(3)過點A作AM⊥CE,垂足為M,根據角的平分線的性質求得AF=AM,然后證得△CAE和△ACM是等腰直角三角形,進而證得EC=2AF.
(1)證明:∵∠ABC+∠ADC=180°,∠ADE+∠ADC=180°,
∴∠ABC=∠ADE,
在△ABC與△ADE中,
 ,
,
∴△ABC≌△ADE(ASA).
(2)證明:∵△ABC≌△ADE,
∴AC=AE,∠BCA=∠E,
∴∠ACD=∠E,
∴∠BCA=∠E=∠ACD,即CA平分∠BCD;
(3)證明:如圖②,過點A作AM⊥CE,垂足為M,
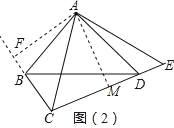
∵AM⊥CD,AF⊥CF,∠BCA=∠ACD,
∴AF=AM,
又∵∠BAC=∠DAE,
∴∠CAE=∠CAD+∠DAE=∠CAD+∠BAC=∠BAD=90°,
∵AC=AE,∠CAE=90°,
∴∠ACE=∠AEC=45°,
∵AM⊥CE,
∴∠ACE=∠CAM=∠MAE=∠E=45°,
∴CM=AM=ME,
又∵AF=AM,
∴EC=2AF.


科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AC,BD相交于點O,O是AC的中點,AD∥BC,AC=8,BD=6,. 
(1)求證:四邊形ABCD是平行四邊形;
(2)若AC⊥BD,求ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣ ![]() x+2
x+2 ![]() 與x軸,y軸分別交于點A,點B,兩動點D,E分別從點A,點B同時出發向點O運動(運動到點O停止),運動速度分別是1個單位長度/秒和
與x軸,y軸分別交于點A,點B,兩動點D,E分別從點A,點B同時出發向點O運動(運動到點O停止),運動速度分別是1個單位長度/秒和 ![]() 個單位長度/秒,設運動時間為t秒,以點A為頂點的拋物線經過點E,過點E作x軸的平行線,與拋物線的另一個交點為點G,與AB相交于點F.
個單位長度/秒,設運動時間為t秒,以點A為頂點的拋物線經過點E,過點E作x軸的平行線,與拋物線的另一個交點為點G,與AB相交于點F.
(1)求點A,點B的坐標;
(2)用含t的代數式分別表示EF和AF的長;
(3)當四邊形ADEF為菱形時,試判斷△AFG與△AGB是否相似,并說明理由.
(4)是否存在t的值,使△AGF為直角三角形?若存在,求出這時拋物線的解析式;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,點E是邊BC的中點,∠AEF=90°,且EF交正方形外角的平分線CF于點F.

(1)求證:AE=EF.
(2)(探究1)變特殊為一般:若題中“點E是邊BC的中點”變為“點E是BC邊上任意一點”,則上述結論是否仍然成立?(填“是”或“否”).
(3)(探究2)在探究1的前提下,若題中結論“AE=EF”與條件“CF是正方形外角的平分線”互換,則命題是否還成立?請給出證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強對校內外安全監控,創建平安校園,某學校計劃增加15臺監控攝像設備,現有甲、乙兩種型號的設備,其中每臺價格,有效監控半徑如表所示,經調查,購買1臺甲型設備比購買1臺乙型設備多150元,購買2臺甲型設備比購買3臺乙型設備少400元.
甲型 | 乙型 | |
價格(元/臺) | a | b |
有效半徑(米/臺) | 150 | 100 |
(1)求a、b的值;
(2)若購買該批設備的資金不超過11000元,且要求監控半徑覆蓋范圍不低于1600米,兩種型號的設備均要至少買一臺,請你為學校設計購買方案,并計算最低購買費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在射線AB上順次取兩點C,D,使AC=CD=1,以CD為邊作矩形CDEF,DE=2,將射線AB繞點A沿逆時針方向旋轉,旋轉角記為α(其中0°<α<45°),旋轉后記作射線AB′,射線AB′分別交矩形CDEF的邊CF,DE于點G,H.若CG=x,EH=y,則下列函數圖象中,能反映y與x之間關系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,O是邊AC上一點,以O為圓心,OA為半徑的圓分別交AB,AC于點E,D,在BC的延長線上取點F,使得BF=EF,EF與AC交于點G.
(1)試判斷直線EF與⊙O的位置關系,并說明理由;
(2)若OA=2,∠A=30°,求圖中陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com