
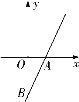
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .點
.點![]() 是該直線上不同于
是該直線上不同于![]() 的點,且
的點,且![]() .
.
(1)寫出![]() 、
、![]() 兩點的坐標;
兩點的坐標;
(2)過動點![]() 且垂直于
且垂直于![]() 軸的直線與直線
軸的直線與直線![]() 交于點
交于點![]() ,若點
,若點![]() 不在線段
不在線段![]() 上,求
上,求![]() 的取值范圍;
的取值范圍;
(3)若直線![]() 與直線
與直線![]() 所夾銳角為
所夾銳角為![]() ,請直接寫出直線
,請直接寫出直線![]() 的函數(shù)解析式.
的函數(shù)解析式.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
解:(1)對于直線![]() ,令
,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ;
;
(2)如解圖①,∵點C在直線![]() 上,且
上,且![]() ,點C不與點B重合,
,點C不與點B重合,
∴點C在BA的右上方,過點C作![]() 軸于點F,
軸于點F,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,![]() ,
,
觀察圖象可知要使過點![]() 且垂直于x軸的直線PD與直線
且垂直于x軸的直線PD與直線![]() 的交點D不在線段BC上,則m的取值范圍為:
的交點D不在線段BC上,則m的取值范圍為:![]() 或
或![]() ;
;

圖①
(3)直線BE的函數(shù)解析式為![]() 或
或![]()
【解法提示】如解圖②,作![]() ,使得
,使得![]() ,作
,作![]() 軸于點H,則
軸于點H,則![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
設(shè)直線BE的函數(shù)解析式為![]() ,
,
將點![]() ,點
,點![]() 分別代入
分別代入
得![]() ,解得
,解得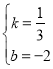 ,
,
∴直線BE的函數(shù)解析式為![]() ,
,
當直線![]() ⊥直線BE時,直線
⊥直線BE時,直線![]() 也滿足條件,
也滿足條件,
∴直線![]() 的函數(shù)解析式為
的函數(shù)解析式為![]() ,
,
∴滿足條件的直線BE的函數(shù)解析式為![]() 或
或![]() .
.

圖②
【思維教練】(1)分別令![]() ,
,![]() 求解;(2)先確定點
求解;(2)先確定點![]() 的位置,過點
的位置,過點![]() 作
作![]() 軸于點
軸于點![]() ,利用全等三角形的性質(zhì),求出點
,利用全等三角形的性質(zhì),求出點![]() 坐標即可求解;(3)直線
坐標即可求解;(3)直線![]() 位置固定,兩條直線夾角為定值時,另一條直線有兩種情況,且由夾角為
位置固定,兩條直線夾角為定值時,另一條直線有兩種情況,且由夾角為![]() ,可知兩種情況下的兩條直線垂直.
,可知兩種情況下的兩條直線垂直.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】數(shù)學(xué)課上,張老師舉了下面的例題:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度數(shù).(答案:
的度數(shù).(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度數(shù).(答案:
的度數(shù).(答案:![]() 或
或![]() 或
或![]() )
)
張老師啟發(fā)同學(xué)們進行變式,小敏編了如下一題:
變式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度數(shù).
的度數(shù).
(1)請你解答以上的變式題.
(2)解(1)后,小敏發(fā)現(xiàn),![]() 的度數(shù)不同,得到
的度數(shù)不同,得到![]() 的度數(shù)的個數(shù)也可能不同.如果在等腰三角形
的度數(shù)的個數(shù)也可能不同.如果在等腰三角形![]() 中,設(shè)
中,設(shè)![]() ,當
,當![]() 有三個不同的度數(shù)時,請你探索
有三個不同的度數(shù)時,請你探索![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
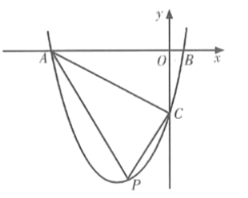
【題目】如圖,在平面直角坐標系中,拋物線![]() 交
交![]() 軸于
軸于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,且
,且![]() ,點
,點![]() 是第三象限內(nèi)拋物線上的一動點.
是第三象限內(nèi)拋物線上的一動點.
(1)求此拋物線的表達式;
(2)若![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)連接![]() ,求
,求![]() 面積的最大值及此時點
面積的最大值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)如圖①,點E在正方形ABCD的內(nèi)部,且EB=EC,過點E畫一條射線平分∠BEC;
(2)如圖②,在△ABC 中,DE∥BC,EF∥AB,請僅用直尺(無刻度)作一個三角形,使所作三角形的面積等于△ABC 面積的一半并把所作的三角形用陰影表示出來.
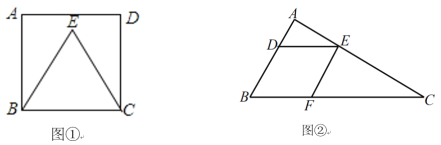
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
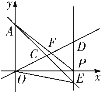
【題目】如圖,在平面直角坐標系中,一次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,與正比例函數(shù)
,與正比例函數(shù)![]() 的圖象交于點
的圖象交于點![]() ,點
,點![]() 在
在![]() 軸的正半軸上,且點
軸的正半軸上,且點![]() 的橫坐標為
的橫坐標為![]() ,過點
,過點![]() 作
作![]() 軸的垂線,分別交一次函數(shù)
軸的垂線,分別交一次函數(shù)![]() 的圖象于點
的圖象于點![]() ,交正比例函數(shù)
,交正比例函數(shù)![]() 的圖象于點
的圖象于點![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)當![]() 為何值時,
為何值時,![]() ;
;
(3)連接![]() 、
、![]() ,
,![]() 交
交![]() 于點
于點![]() ,已知
,已知![]() ,在討論
,在討論![]() 的面積與
的面積與![]() 面積的大小問題時,嘉嘉認為
面積的大小問題時,嘉嘉認為![]() ,淇淇認為
,淇淇認為![]() ,請你作為小法官,幫助他們兩人評判,誰的說法正確.
,請你作為小法官,幫助他們兩人評判,誰的說法正確.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,2×2網(wǎng)格(每個小正方形的邊長為1)中有A,B,C,D,E,F,G,H,O九個格點.拋物線l的解析式為y=(-1)nx2+bx+c(n為整數(shù)).

(1)n為奇數(shù),且l經(jīng)過點H(0,1)和C(2,1),求b,c的值,并直接寫出哪個格點是該拋物線上的頂點;
(2)n為偶數(shù),且l經(jīng)過點A(1, 0)和B(2,0),通過計算說明點F(0,2)和H(0,1)是否在拋物線上;
(3)若l經(jīng)過這九個格點中的三個,直接寫出滿足這樣條件的拋物線條數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)![]() 的圖象
的圖象![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() :
:![]() 與
與![]() 軸的交點分別為
軸的交點分別為![]() 、
、![]() (點
(點![]() 在點
在點![]() 的左側(cè)).
的左側(cè)).

(1)當![]() 的頂點在
的頂點在![]() 上時,求
上時,求![]() 的值;
的值;
(2)若![]() 、
、![]() 兩點中有一點與點
兩點中有一點與點![]() 關(guān)于原點對稱,試判斷這個點是點
關(guān)于原點對稱,試判斷這個點是點![]() 還是點
還是點![]() ;
;
(3)若![]() 的頂點為
的頂點為![]() ,對稱軸與
,對稱軸與![]() 的交點為
的交點為![]() ,且點
,且點![]() 在點
在點![]() 的下方,當
的下方,當![]() 為何值時,線段
為何值時,線段![]() 的長最大.
的長最大.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
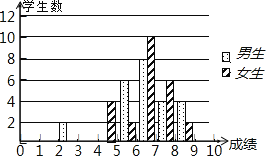
【題目】為了迎接體育中考,初三7班的體育老師對全班48名學(xué)生進行了一次體能模擬測試,得分均為整數(shù),滿分10分,成績達到6分以上(包括6分)為合格,成績達到9分以上(包括9分)為優(yōu)秀,這次模擬測試中男、女生全部成績分布的條形統(tǒng)計圖如下
(1)請補充完成下面的成績統(tǒng)計分析表:
平均分 | 方差 | 中位數(shù) | 合格率 | 優(yōu)秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
(2)男生說他們的合格率、優(yōu)秀率均高于女生,所以他們的成績好于女生,但女生不同意男生的說法,認為女生的成績要好于男生,請給出兩條支持女生觀點的理由;
(3)體育老師說,咱班的合格率基本達標,但優(yōu)秀率太低,我們必須加強體育鍛煉,兩周后的目標是:全班優(yōu)秀率達到50%.如果女生新增優(yōu)秀人數(shù)恰好是男生新增優(yōu)秀人數(shù)的兩倍,那么男、女生分別新增多少優(yōu)秀人數(shù)才能達到老師的目標?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com