
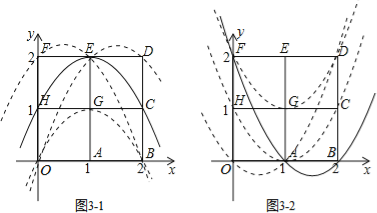
【題目】如圖,2×2網格(每個小正方形的邊長為1)中有A,B,C,D,E,F,G,H,O九個格點.拋物線l的解析式為y=(-1)nx2+bx+c(n為整數).

(1)n為奇數,且l經過點H(0,1)和C(2,1),求b,c的值,并直接寫出哪個格點是該拋物線上的頂點;
(2)n為偶數,且l經過點A(1, 0)和B(2,0),通過計算說明點F(0,2)和H(0,1)是否在拋物線上;
(3)若l經過這九個格點中的三個,直接寫出滿足這樣條件的拋物線條數.
【答案】(1)b=2,c=1. 頂點所在的格點為E.(2)F點在該拋物線上,H點不在該拋物線上.(3)8.
【解析】試題分析:(1)根據-1的奇數次方等于-1,再把點H、C的坐標代入拋物線解析式計算即可求出b、c的值,然后把函數解析式整理成頂點式形式,寫出頂點坐標即可;
(2)根據-1的偶數次方等于1,再把點A、B的坐標代入拋物線解析式計算即可求出b、c的值,從而得到函數解析式,再根據拋物線上點的坐標特征進行判斷;
(3)分別利用(1)(2)中的結論,將拋物線平移,可以確定拋物線的條數.
試題解析:(1)n為奇數時,y=-x2+bx+c,
∵l經過點H(0,1)和C(2,1),
∴![]() ,
,
解得![]() ,
,
∴拋物線解析式為y=-x2+2x+1,
y=-(x-1)2+2,
∴頂點為格點E(1,2);
(2)n為偶數時,y=x2+bx+c,
∵l經過點A(1,0)和B(2,0),
∴![]() ,
,
解得![]() ,
,
∴拋物線解析式為y=x2-3x+2,
當x=0時,y=2,
∴點F(0,2)在拋物線上,點H(0,1)不在拋物線上;
(3)所有滿足條件的拋物線共有8條.
當n為奇數時,由(1)中的拋物線平移又得到3條拋物線,如答圖3-1所示;
當n為偶數時,由(2)中的拋物線平移又得到3條拋物線,如答圖3-2所示.


科目:初中數學 來源: 題型:
【題目】下列四個命題中:
①在同一平面內,互相垂直的兩條直線一定相交
②有且只有一條直線垂直于已知直線
③兩條直線被第三條直線所截,同位角相等
④從直線外一點到這條直線的垂線段,叫做這點到這條直線的距離.
其中真命題的個數為( )
A. 1個 B. 2 個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場自行車存放處每周的存車量為5000輛次,其中變速車存車費是每輛一次1元,普通車存車費為每輛一次0.5元,若普通車存車量為x輛次,存車的總收入為y元,則y與x之間的關系式是( )
A. y=0.5x+5000 B. y=0.5x+2500 C. y=﹣0.5x+5000 D. y=﹣0.5x+2500
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=5,BC=6,AD為BC邊上的高,過點A作AE∥BC,過點D作DE∥AC,AE與DE交于點E,AB與DE交于點F,連結BE.求四邊形AEBD的面積

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各組數中:①-22與(-2)2; ②(-3)2與-33; ③-(-32)與-32 ;④02019與02018;⑤(-1)2019與-(-1)2.其中結果相等的數據共有( )
A.1對B.2對C.3對D.4對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】嘉淇同學用配方法推導一元二次方程ax2+bx+c=0(a≠0)的求根公式時,對于b2﹣4ac>0的情況,她是這樣做的:
由于a≠0,方程ax2+bx+c=0變形為:
x2+![]() x=﹣
x=﹣![]() ,…第一步
,…第一步
x2+![]() x+(
x+(![]() )2=﹣
)2=﹣![]() +(
+(![]() )2,…第二步
)2,…第二步
(x+![]() )2=
)2=![]() ,…第三步
,…第三步
x+![]() =
=![]() (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步
x=![]() ,…第五步
,…第五步
嘉淇的解法從第 步開始出現錯誤;事實上,當b2﹣4ac>0時,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com