
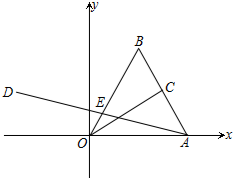
 如圖,在平面直角坐標系中,A(8,0),點B在第一象限,△OAB為等邊三角形,OC⊥AB,垂足為點C.
如圖,在平面直角坐標系中,A(8,0),點B在第一象限,△OAB為等邊三角形,OC⊥AB,垂足為點C.分析 (1)如圖1所示:過點B作BF⊥OA,垂足為F.由等腰三角形三線合一的性質可知OF=AF=4、BC=AC,由等邊三角形的性質可知:∠BOF=60°,由特殊銳角三角函數值可知;FB=4$\sqrt{3}$,從而得到點B的坐標為(4,4$\sqrt{3}$),由中點坐標公式可知點C的坐標為(6,2$\sqrt{3}$);
(2)方法1:設OB的解析式為y=kx,將點B的坐標代入得:k=$\sqrt{3}$,于是得到直線OB的解析式為y=$\sqrt{3}x$.由關于y軸對稱的點的坐標特點可求得點D的坐標,然后依據待定系數法可求得直線AD的解析式為y=$-\frac{\sqrt{3}}{7}x+\frac{8\sqrt{3}}{7}$.將y=$\sqrt{3}x$代入y=$-\frac{\sqrt{3}}{7}x+\frac{8\sqrt{3}}{7}$可求得點E的坐標為(1,$\sqrt{3}$).由兩點間的距離公式可知:OE=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2;
方法2:連接CD,交OB于F.由關于y軸對稱對稱的點坐標坐標特點可知:CD∥OA,D(-6,2$\sqrt{3}$),從而得到DC=12,由題意可知△BCF為等邊三角形,從而得到CF=4,然后可求得DF=12-4=8=OA,依據AAS可證明△DEF≌△AEO(AAS),由全等三角形的性質可知OE=EF,從而可求得OE=2;
(3)如圖3,連接PB.依據SAS可證明△HAO≌△PAB,由全等三角形的性質可知:OH=PB,由垂線段最短的性質可知:當BP⊥y軸時,PB有最小值為4,由PB⊥y軸可知∠AOH=∠ABP=120°,從而得到∠COH=60°,過點H作HC⊥x軸于C,由OH=4,∠COH=60°,可求得OC=2.
解答 解:(1)如圖1所示:過點B作BF⊥OA,垂足為F.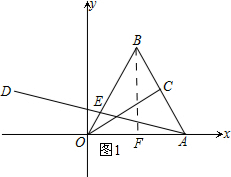
∵OB=AB,BF⊥OA,
∴OF=AF=4.
∵△OAB為等邊三角形,
∴∠BOF=60°.
∴FB=OBsin60°=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$.
∴點B的坐標為(4,4$\sqrt{3}$).
∵AO=OB,OC⊥AB,
∴BC=AC.
由中點坐標公式可知點C的坐標為(6,2$\sqrt{3}$).
故答案為:6.
(2)方法1:設OB的解析式為y=kx,將點B的坐標代入得:4k=4$\sqrt{3}$,
解得:k=$\sqrt{3}$.
∴直線OB的解析式為y=$\sqrt{3}x$.
∵點C與點D關于y軸對稱,
∴點D的坐標為(-6,2$\sqrt{3}$).
設DA的解析式為y=k1x+b.將點A和點D的坐標代入得:$\left\{\begin{array}{l}{8{k}_{1}+b=0}\\{-6{k}_{1}+b=2\sqrt{3}}\end{array}\right.$,
解得:k1=-$\frac{\sqrt{3}}{7}$,b=$\frac{8\sqrt{3}}{7}$.
∴直線DA的解析式為y=$-\frac{\sqrt{3}}{7}x+\frac{8\sqrt{3}}{7}$.
將y=$\sqrt{3}x$代入y=$-\frac{\sqrt{3}}{7}x+\frac{8\sqrt{3}}{7}$得:$\sqrt{3}x+\frac{\sqrt{3}}{7}x=\frac{8\sqrt{3}}{7}$.
解得:x=1.
∴y=$\sqrt{3}$.
∴點E的坐標為(1,$\sqrt{3}$).
由兩點間的距離公式可知:OE=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2.
方法2:如圖2所示:連接CD,交OB于F.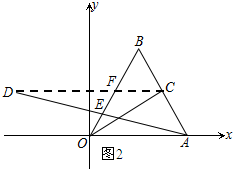
∵點C與點D關于y軸對稱,
∴CD∥OA,點D(-6,2$\sqrt{3}$).
∴△BCF為等邊三角形,
∴CF=4,CD=12.
∴DF=12-4=8=OA.
在△DEF和△AEO中,
$\left\{\begin{array}{l}∠DFE=∠AOE\\∠DEF=∠AEO\\ DF=AP\end{array}\right.$
∴△DEF≌△AEO(AAS),
∴OE=EF=$\frac{1}{2}$OF,
∵BF=BC=4,
∴OF=4,
∴OE=2.
(3)如圖3,連接PB.
∵∠HAO+∠PAO=∠BAP+∠PAO=60°,
∴∠HAO=∠PAB,
在△HAO和△PAB中,
$\left\{\begin{array}{l}AH=AP\\∠HAO=∠PAB\\ OA=BA\end{array}\right.$
∴△HAO≌△PAB(SAS),
∴OH=PB,
當BP⊥y軸時,PB有最小值為4,此時,∠AOH=∠ABP=120°,
∴∠COH=60°
過點H作HC⊥x軸于C,
∵OH=4,∠COH=60°,
∴OC=2,即H點橫坐標為-2.
點評 本題主要考查的是一次函數的綜合應用,解答本題主要應用了待定系數法求一次函數的解析式、全等三角形的性質和判定、特殊銳角三角函數、垂線段的性質、等邊三角形的性質,證得當BP⊥y軸時,OH有最小值是解題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
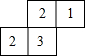 由若干個小正方形搭成幾何體,從上面看到的幾何體的形狀如圖所示,其中小方格中的數字表示在該位置的小正方體的個數,請在指定位置畫出該幾何體從正面看和從左面看得到的幾何體的形狀圖.
由若干個小正方形搭成幾何體,從上面看到的幾何體的形狀如圖所示,其中小方格中的數字表示在該位置的小正方體的個數,請在指定位置畫出該幾何體從正面看和從左面看得到的幾何體的形狀圖.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com