
 如圖,將一副三角尺的直角頂點疊放在點C處,∠D=30°,∠B=45°,求:
如圖,將一副三角尺的直角頂點疊放在點C處,∠D=30°,∠B=45°,求:分析 (1))由∠ACD=∠BCE=90°,根據圖形可知∠ACB=180°-∠DCE;
(2)由∠ACD=∠BCE=90°,根據圖形可知∠DCE=180°-∠ACB;
(3)由∠ACD=∠BCE=90°,得出∠ACE+∠DCE+∠DCE+∠BCD=180°,即可證出∠ACB+∠DCE=180°.
解答 解:(1)∵∠ECB=90°,∠DCE=35°
∴∠DCB=90°-35°=55°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=145°.
(2)∵∠ACB=120°,∠ACD=90°
∴∠DCB=120°-90°=30°
∵∠ECB=90°
∴∠DCE=90°-30°=60°.
(3)猜想得∠ACB+∠DCE=180°(或∠ACB與∠DCE互補)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB-∠DCB=90°-∠DCB
∴∠ACB+∠DCE=180°.
點評 本題考查了余角和補角的定義;弄清兩個角之間的互余和互補關系是解題的關鍵.


 華東師大版一課一練系列答案
華東師大版一課一練系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
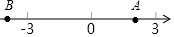 點A、B在數軸上的位置如圖所示,其對應的數分別是a和b,對于以下結論:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正確的是( )
點A、B在數軸上的位置如圖所示,其對應的數分別是a和b,對于以下結論:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正確的是( )| A. | 甲乙 | B. | 甲丙 | C. | 丙丁 | D. | 乙丁 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2017,$\frac{1}{2017}$ | B. | $-\frac{1}{2017}$,2017 | C. | 2017,$-\frac{1}{2017}$ | D. | -2017,$\frac{1}{2017}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
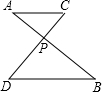 如圖,線段AB與CD相交于點P,AC∥BD,∠A=39°,∠D=50°,則( )
如圖,線段AB與CD相交于點P,AC∥BD,∠A=39°,∠D=50°,則( )| A. | ∠APD=39° | B. | ∠APD=50° | C. | ∠APD=89° | D. | ∠APD=76° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com