
(12分)如圖1,在△ABC中,AC=AB=2,∠A=90°,將一塊與△ABC全等的三角板的直角頂點放在點C上,一直角邊與BC重疊.
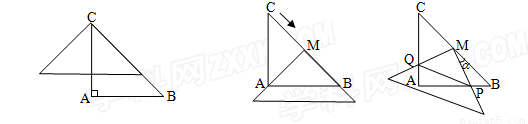
(1)操作1:固定△ABC,將三角板沿 方向平移,使其直角頂點落在BC的中點M,如圖2所示,探究:三角板沿
方向平移,使其直角頂點落在BC的中點M,如圖2所示,探究:三角板沿 方向平移的距離為___________;
方向平移的距離為___________;
(2)操作2:在(1)的情況下,將三角板BC的中點M順時針方向旋轉角度 ,如圖3所示,探究:設三角形板兩直角邊分別與AB、AC交于點P、Q,觀察四邊形MPAQ形狀的變化,問:四邊形MPAQ的面積S是否改變,若不變,求其面積;若改變,試說明理由;
,如圖3所示,探究:設三角形板兩直角邊分別與AB、AC交于點P、Q,觀察四邊形MPAQ形狀的變化,問:四邊形MPAQ的面積S是否改變,若不變,求其面積;若改變,試說明理由;
(3)在(2)的情形下,連PQ,設BP=x,記△MPQ的面積為y,試求y關于x的函數關系式,并求x為何值時,y的值是四邊形MPAQ的面積的一半,此時,指出四邊形MPAQ的形狀.
(1) ;(2)不變,1;(2)
;(2)不變,1;(2) ,當
,當 時,MPAQ為正方形.
時,MPAQ為正方形.
【解析】
試題分析:(1)M是BC的中點,三角板沿C→B方向平移的距離為CM,根據勾股定理可求BC,那么CM可求;
(2)連AM,分別證明△MAQ≌△MBP和△MAP≌△MCQ,那么四邊形MPAQ的面積S就是△ABC面積的一半;
(3)用四邊形MPAQ的面積減去△APQ可得△MPQ的面積,而AQ=PB=x,AP=2﹣x,據此列出y關于x的函數關系式,將函數值代入函數關系式可得自變量,根據自變量可以判斷四邊形MPAQ的形狀.
試題解析:(1)BC= ,∴CM=
,∴CM= BC=
BC= ,故三角板沿C→B方向平移的距離為:
,故三角板沿C→B方向平移的距離為: ;
;
(2)四邊形MPAQ的面積S不變,如圖,連AM,M是等腰直角三角形ABC斜邊BC的中點,

∴AM=BM,而∠QMA=∠PMB=a,∠QAM=∠PBM=45°,∴△MAQ≌△MBP,
同理可得:△MAP≌△MCQ,
∴S四邊形MPAQ=S△MAQ+S△MAP= S△ABC=
S△ABC= ;
;
(3) ,如果y的值是四邊形MPAQ的面積的一半,
,如果y的值是四邊形MPAQ的面積的一半,
則有: ,解得,
,解得, .
.
當 時,即BP=1,∵AB=2,∴AP=1,
時,即BP=1,∵AB=2,∴AP=1,
∵y的值是四邊形MPAQ的面積的一半,∴△PAQ的面積=△PMQ的面積= ,∴QA=1,
,∴QA=1,
∵△MAQ≌△MBP,∴QM=MP,∴QM=MP=1,∴QM=MP=QA=AP=1,
∵∠PAQ=90°,∴四邊形MPAQ為正方形.
考點:1.旋轉的性質;2.全等三角形的判定與性質;3.正方形的判定;4.平移的性質.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源:2014-2015學年福建省、三中、城關小學九年級上學期期中聯考數學試卷(解析版) 題型:選擇題
如圖所示,在平面直角坐標系中,二次函數 (
(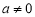 )的圖象過正方形ABOC的三頂點A、B、C,則
)的圖象過正方形ABOC的三頂點A、B、C,則 的值是 .
的值是 .

查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期期中質量監測數學試卷(解析版) 題型:選擇題
如圖,在正方形ABCD中,E為DC邊上的點,連接BE,將ΔBCE繞點C順時針方向旋轉90°得到ΔDCF,連接EF,若∠BEC=60°,則∠ EFD的度數為( )

A.10° B.15° C.20° D.25°
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期期中質量監測數學試卷(解析版) 題型:解答題
(8分)如圖,在直角梯形紙片ABCD中,AB∥DC,∠A=90°,CD>AD,將紙片沿過點D的直線折疊,使點A落在邊CD上的點E處,折痕為DF.連接EF并展開紙片.
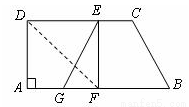
(1)求證:四邊形ADEF是正方形;
(2)取線段AF的中點G,連接EG,如果BG=CD,試說明四邊形GBCE是等腰梯形.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省龍巖市七年級上學期半期考試數學試卷(解析版) 題型:選擇題
一個數的平方和它的倒數相等,則這個數是:( )
A.1 B.-1 C. ±1 D.±1和0[
查看答案和解析>>
科目:初中數學 來源:2014-2015學年遼寧大石橋水源鎮二中七年級上學期期末模擬數學試卷(解析版) 題型:選擇題
買一個足球需要 元,買一個籃球需要
元,買一個籃球需要 元,則買4個足球、7個籃球共需要( )元。
元,則買4個足球、7個籃球共需要( )元。
A.4m+7n B.28mn C.7m+4n D.11mn
查看答案和解析>>
科目:初中數學 來源:2014-2015學年遼寧大石橋湯池鎮一中七年級上學期期末模擬數學試卷(解析版) 題型:選擇題
冥王星圍繞太陽公轉的軌道半徑長度約為5 900 000 000千米,這個數用科學記數法表示是( )
A.5.9×1010千米 B.5.9×109千米
C.59×108千米 D.0.59×1010千米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com