
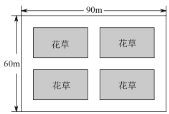
【題目】成都市中心城區“小游園,微綠地”規劃已經實施,武侯區某街道有一塊矩形空地進入規劃試點.如圖,已知該矩形空地長為![]() ,寬為
,寬為![]() ,按照規劃將預留總面積為
,按照規劃將預留總面積為![]() 的四個小矩形區域(陰影部分)種植花草,并在花草周圍修建三條橫向通道和三條縱向通道,各通道的寬度相等.
的四個小矩形區域(陰影部分)種植花草,并在花草周圍修建三條橫向通道和三條縱向通道,各通道的寬度相等.
(1)求各通道的寬度;
(2)現有一工程隊承接了對這![]() 的區域(陰影部分)進行種植花草的綠化任務,該工程隊先按照原計劃進行施工,在完成了
的區域(陰影部分)進行種植花草的綠化任務,該工程隊先按照原計劃進行施工,在完成了![]() 的綠化任務后,將工作效率提高
的綠化任務后,將工作效率提高![]() ,結果提前
,結果提前![]() 天完成任務,求該工程隊原計劃每天完成多少平方米的綠化任務?
天完成任務,求該工程隊原計劃每天完成多少平方米的綠化任務?
【答案】(1)各通道的寬度為![]() 米;(2)原計劃每天完成
米;(2)原計劃每天完成![]() 平方米的綠化任務.
平方米的綠化任務.
【解析】
(1)設各通道的寬度為x米,將四個小矩形合并成一個大矩形,則大矩形的長為(90-3x)cm,寬為(60-3x)cm,再根據矩形面積公式列方程求解即可;
(2)設該工程隊原計劃每天完成ym2的綠化任務,則按原計劃完成任務需要![]() 天,完成
天,完成![]() 的綠化任務需要
的綠化任務需要![]() 天,提高工作效率后完成剩余工作量所需要的時間為
天,提高工作效率后完成剩余工作量所需要的時間為![]() 天,再按照題干所給時間關系列出方程并求解即可.
天,再按照題干所給時間關系列出方程并求解即可.
解:(1)設各通道的寬度為x米,將四個小矩形合并成一個大矩形,則可得方程,
(90-3x)(60-3x)=4536,解得x=2或48(不合題意,舍去),
故各通道的寬度為![]() 米;
米;
(2)設該工程隊原計劃每天完成ym2的綠化任務,則由題干條件得,
![]() ,解得y=400m2/天,
,解得y=400m2/天,
經檢驗,y=400m2/天是原方程的解,并符合題意,
故原計劃每天完成![]() 平方米的綠化任務.
平方米的綠化任務.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
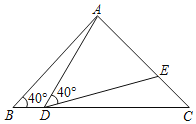
【題目】如圖,在△ABC中,AB=AC=2,∠B=40°,點D在線段BC上運動(D不與B、C重合),連接AD,作∠ADE=40°,DE與AC交于E.
(1)當∠BDA=115°時,∠BAD=_____°,∠DEC=_____°;當點D從B向C運動時,∠BDA逐漸變______(填”大”或”小”);
(2)當DC=AB=2時,△ABD與△DCE是否全等?請說明理由:
(3)在點D的運動過程中,△ADE的形狀可以是等腰三角形嗎?若可以,請直接寫出∠BDA的度數;若不可以,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A、B、C、D為矩形的四個頂點,AB=16cm,AD=6cm,動點P、Q分別從點A、C同時出發,點P以3cm/s的速度向點B移動,一直到達B為止,點Q以2 cm/s的速度向D移動.
(1)P、Q兩點從出發開始到幾秒?四邊形PBCQ的面積為33cm2;
(2)P、Q兩點從出發開始到幾秒時?點P和點Q的距離是10cm.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個口袋有![]() 個黑球和若干個白球,在不允許將球倒出來的前提下,小明為估計其中的白球數,采用了如下的方法:從口袋中隨機摸出一球,記下顏色,然后把它放回口袋中,搖勻后再隨機摸出一球,記下顏色,再放回口袋中,…,不斷重復上述過程,小明共摸了
個黑球和若干個白球,在不允許將球倒出來的前提下,小明為估計其中的白球數,采用了如下的方法:從口袋中隨機摸出一球,記下顏色,然后把它放回口袋中,搖勻后再隨機摸出一球,記下顏色,再放回口袋中,…,不斷重復上述過程,小明共摸了![]() 次,其中
次,其中![]() 次摸到黑球.根據上述數據,小明正估計口袋中的白球的個數是________.
次摸到黑球.根據上述數據,小明正估計口袋中的白球的個數是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E是AB上一點,F是AD延長線上一點,且DF=BE.

(1)求證:CE=CF;
(2)若點G在AD上,且∠GCE=45°,則GE=BE+GD成立嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
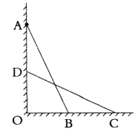
【題目】王涵想知道一堵墻上點![]() 的高度,即
的高度,即![]() 的長度
的長度![]() ,但點
,但點![]() 的位置較高,沒有梯子之類的工具,于是設計了下面的方案,請你先補全方案,再說明理由.
的位置較高,沒有梯子之類的工具,于是設計了下面的方案,請你先補全方案,再說明理由.
(1)補全方案.
第一步:如圖,找一根長度大于![]() 的直桿,使直桿靠在墻上,且頂端與點
的直桿,使直桿靠在墻上,且頂端與點![]() 重合,記下直桿與地面的夾角
重合,記下直桿與地面的夾角![]() ;
;
第二步:使直桿頂端豎直緩慢下滑,直到![]() __________
__________![]() __________,標記此時直桿的底端點
__________,標記此時直桿的底端點![]() ;
;
第三步:測量__________的長度,即為點![]() 的高度;
的高度;
(2)說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(解決問題)已知![]() ,
,![]() ,
,![]() 是同一平面上的三個點,以線段
是同一平面上的三個點,以線段![]() ,
,![]() 為邊,分別作正三角形
為邊,分別作正三角形![]() 和正三角形
和正三角形![]() ,連接
,連接![]() ,
,![]() .
.
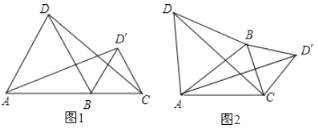
(1)如圖1,當點![]() ,
,![]() ,
,![]() 在同一直線上時,線段
在同一直線上時,線段![]() 與
與![]() 的大小關系是__________;
的大小關系是__________;
(2)如圖2,當![]() ,
,![]() ,
,![]() 為三角形的頂點時(點
為三角形的頂點時(點![]() ,
,![]() ,
,![]() 不在同一條直線上),判斷線段
不在同一條直線上),判斷線段![]() 與
與![]() 的大小關系是否發生改變,并說明理由;
的大小關系是否發生改變,并說明理由;
(類比猜想)
(3)已知![]() ,
,![]() ,
,![]() 是同一平面上的三個點,以線段
是同一平面上的三個點,以線段![]() ,
,![]() 為邊,分別作正方形,連接
為邊,分別作正方形,連接![]() ,
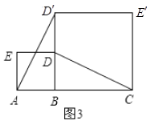
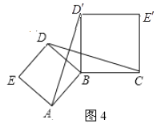
,![]() ,如圖3和圖4所示.判斷線段
,如圖3和圖4所示.判斷線段![]() 與
與![]() 的大小關系,并在圖4(點
的大小關系,并在圖4(點![]() ,
,![]() ,
,![]() 不在同一條直線上)中證明你的判斷;
不在同一條直線上)中證明你的判斷;
(推廣應用)(4)上面的這些結論能否推廣到任意正多邊形(不必證明)?
(5)如圖5,![]() 與
與![]() 的大小關系是__________,并寫出它們分別在哪兩個全等三角形中;
的大小關系是__________,并寫出它們分別在哪兩個全等三角形中;
(6)請在圖6中連接圖中兩個頂點,構造處一組全等三角形,并寫出這兩個全等的三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
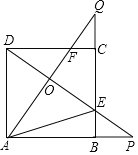
【題目】如圖,正方形ABCD的邊長是![]() ,連接
,連接![]() 交于點O,并分別與邊
交于點O,并分別與邊![]() 交于點
交于點![]() ,連接AE,下列結論:
,連接AE,下列結論: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 當
當![]() 時,
時, ![]() ,其中正確結論的個數是
,其中正確結論的個數是![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】901班的全體同學根據自己的興趣愛好參加了六個學生社團(每個學生必須參加且只參加一個),為了了解學生參加社團的情況,學生會對該班參加各個社團的人數進行了統計,繪制成了如圖不完整的扇形統計圖,已知參加“讀書社”的學生有15人,請解答下列問題:
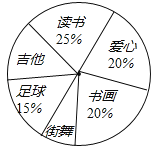
(1)該班的學生共有 名;
(2)若該班參加“吉他社”與“街舞社”的人數相同,請你計算,“吉他社”對應扇形的圓心角的度數;
(3)901班學生甲、乙、丙是“愛心社”的優秀社員,現要從這三名學生中隨機選兩名學生參加“社區義工”活動,請你用畫樹狀圖或列表的方法求出恰好選中甲和乙的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com