
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,拋物線的對稱軸與
,拋物線的對稱軸與![]() 軸交于點
軸交于點![]() ,頂點坐標為
,頂點坐標為![]() .
.
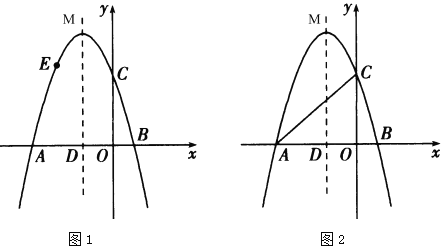
(1)求拋物線的表達式和頂點![]() 的坐標;
的坐標;
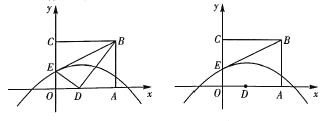
(2)如圖1,點![]() 為拋物線上一點,點
為拋物線上一點,點![]() 不與點
不與點![]() 重合,當
重合,當![]() 時,過點
時,過點![]() 作
作![]() 軸,交拋物線的對稱軸于點
軸,交拋物線的對稱軸于點![]() ,作
,作![]() 軸于點H,得到矩形
軸于點H,得到矩形![]() ,求矩形
,求矩形![]() 的周長的最大值;
的周長的最大值;
(3)如圖2,點![]() 為拋物線對稱軸上一點,是否存在點
為拋物線對稱軸上一點,是否存在點![]() ,使以點
,使以點![]() 、
、![]() 、
、![]() 為頂點的三角形是直角三角形?若存在,求出點
為頂點的三角形是直角三角形?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ,頂點坐標
,頂點坐標![]() ;(2)周長的最大值為
;(2)周長的最大值為![]() ;(3)存在,P的坐標為
;(3)存在,P的坐標為![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)把A、B坐標代入y=-x2+bx+c,解方程組求出b、c的值即可得答案;(2)設矩形![]() 的周長為
的周長為![]() ,
,![]() ,分別討論-7<x<-3時和-3<x<-2時兩種情況,用x表示出矩形的周長,根據二次函數的性質求出最大值即可得答案;(3)設
,分別討論-7<x<-3時和-3<x<-2時兩種情況,用x表示出矩形的周長,根據二次函數的性質求出最大值即可得答案;(3)設![]() 分
分![]() 時,
時,![]() 時,
時,![]() 時,三種情況討論,利用勾股定理求出m的值即可得答案.
時,三種情況討論,利用勾股定理求出m的值即可得答案.
(1)把![]() 兩點坐標代入
兩點坐標代入![]()
得![]() ,
,
解得:![]() ,
,
∴拋物線方程為:![]() ,頂點坐標
,頂點坐標![]() ,
,
(2)
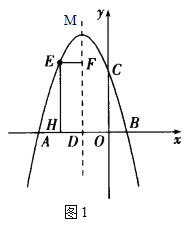
如圖1,設矩形![]() 的周長為
的周長為![]() ,
,![]() ,
,
∴![]() ,
,
∵A(-7,0),B(1,0),
∴拋物線對稱軸為直線x=-3,
①當![]() 時,
時,
![]() ,
,
![]() ,
,
=![]()
=![]()
=![]()
=![]()
![]()
∵![]() ,
,
∴![]() 時,矩形周長最大,最大值為
時,矩形周長最大,最大值為![]() .
.
②當![]() 時
時
EF=x-(-3)=x+3,
l=![]()
=![]()
![]() .
.
∴當![]() 時,矩形周長最大,最大值為
時,矩形周長最大,最大值為![]()
∴綜上所述,周長的最大值為![]()
(3)存在.如下圖
設![]()
(i)當![]() 時,
時,![]()
16+![]()
16![]()
2![]()
m2![]()
解得:![]()
∴P1![]() ,P2
,P2![]()
(ii)當![]() 時,
時,![]()
49+49+9+(7-m)2=16+m2
∴![]()
140=14m,
m=10,
∴P3![]() ,
,
(iii)當![]() 時,
時,![]()
98+16+m2=9+(7-m)2
49+49+16+m2=9+49-14m+m2
56=-14m
解得:![]() ,
,
∴P4![]()
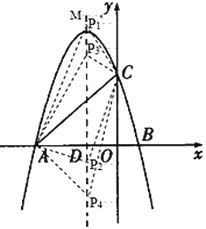
綜上所述:滿足條件的點P的坐標為![]() ,
,![]() ,
,![]() ,
,![]()


科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為邊在
為邊在![]() 的另一側作
的另一側作![]() ,點
,點![]() 為射線
為射線![]() 上任意一點,在射線
上任意一點,在射線![]() 上截取
上截取![]() ,連接
,連接![]() 、
、![]() 、
、![]() .
.
(1)如圖1,當點![]() 落在線段
落在線段![]() 的延長線上時,求
的延長線上時,求![]() 的度數;
的度數;
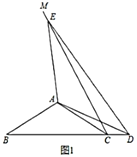
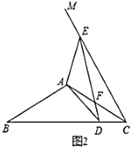
(2)如圖2,當點![]() 落在線段
落在線段![]() (不含邊界)上時,
(不含邊界)上時,![]() 與
與![]() 交于點
交于點![]() ,請問(1)中的結論是否仍成立?如果成立,請給出證明;如果不成立,請說明理由;
,請問(1)中的結論是否仍成立?如果成立,請給出證明;如果不成立,請說明理由;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲口袋中裝有2個相同的小球,它們分別寫有數值![]() ;乙口袋中裝有3個相同的小球,它們分別寫有數值
;乙口袋中裝有3個相同的小球,它們分別寫有數值![]() .現從甲口袋中隨機取一球,記它上面的數值為
.現從甲口袋中隨機取一球,記它上面的數值為![]() ,再從乙口袋中隨機取一球,記它上面的數值為
,再從乙口袋中隨機取一球,記它上面的數值為![]() .設點
.設點![]() 的坐標為
的坐標為![]() .
.
(1)請用樹狀圖或列表法,列出![]() 所有可能的結果;
所有可能的結果;
(2)求點![]() 落在第一象限的概率.
落在第一象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】科幻小說《實驗室的故事》中,有這樣一個情節,科學家把一種珍奇的植物分別放在不同溫度的環境中,經過一天后,測試出這種植物高度的增長情況(如表):
溫度 | …… |
|
| 0 | 2 | 4 | 4.5 | …… |
植物每天高度增長量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由這些數據,科學家推測出植物每天高度增長量![]() 是溫度
是溫度![]() 的函數,且這種函數是一次函數和二次函數中的一種.
的函數,且這種函數是一次函數和二次函數中的一種.
(1)請你選擇一種適當的函數,求出它的函數關系式,并簡要說明不選擇另外一種函數的理由;
(2)如果實驗室溫度保持不變,在10天內要使該植物高度增長量的總和超過![]() ,那么實驗室的溫度
,那么實驗室的溫度![]() 應該在哪個范圍內選擇?請說明理由.
應該在哪個范圍內選擇?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上,點A表示1,現將點A沿數軸做如下移動,第一次將點A向左移動3個單位長度到達點A1,第二次將點A1向右移動6個單位長度到達點A2,第三次將點A2向左移動9個單位長度到達點A3,…按照這種移動規律進行下去,第51次移動到點A51,那么點A51所表示的數為( )
![]()
A. ﹣74 B. ﹣77 C. ﹣80 D .﹣83
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一組等距的平行線,點A、B、C分別在直線l1、l6、l4上,AB交l3于點D,AC交l3于點E,BC交于l5點F,若△DEF的面積為1,則△ABC的面積為_____.
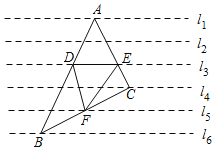
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的三個頂點分別為A(1,2),B(2,5),C(6,1).若函數y=![]() 在第一象限內的圖象與△ABC有交點,則k的取值范圍是_____.
在第一象限內的圖象與△ABC有交點,則k的取值范圍是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2016廣西賀州市)如圖,將線段AB繞點O順時針旋轉90°得到線段A′B′,那么A(﹣2,5)的對應點A′的坐標是( )
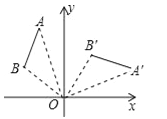
A. (2,5) B. (5,2) C. (2,﹣5) D. (5,﹣2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,若折疊矩形![]() 的一邊
的一邊![]() ,使點
,使點![]() 落在
落在![]() 邊的點
邊的點![]() 處,已知折痕
處,已知折痕![]() 且.以
且.以![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸建立如圖所示的平面直角坐標系,拋物線
軸建立如圖所示的平面直角坐標系,拋物線![]() 經過點
經過點![]() .
.
(1)求![]() 的值;
的值;
(2)點![]() 是線段
是線段![]() 上一動點,點
上一動點,點![]() 在拋物線上,且始終滿足
在拋物線上,且始終滿足![]() ,在點
,在點![]() 運動過程中,能否使得
運動過程中,能否使得![]() ?若能,求出所有符合條件的點
?若能,求出所有符合條件的點![]() 的坐標;若不能,請說明理由;
的坐標;若不能,請說明理由;
(3)已知點![]() 是拋物線上一動點,點
是拋物線上一動點,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,若在
,若在![]() 軸上存在一點
軸上存在一點![]() ,使
,使![]() 有最小值,求點
有最小值,求點![]() 的縱坐標的最大值.
的縱坐標的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com