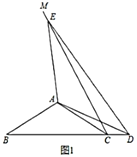
【題目】在
中，
，
，以
為邊在
的另一側作
，點
為射線
上任意一點，在射線
上截取
，連接
、
、
．
（1）如圖1，當點落在線段的延長線上時，求
的度數；
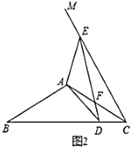
（2）如圖2，當點落在線段(不含邊界)上時，
與交于點
，請問（1）中的結論是否仍成立？如果成立，請給出證明；如果不成立，請說明理由；
閱讀快車系列答案科目：初中數學 來源： 題型：
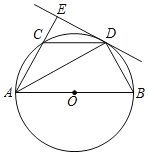
【題目】如圖，AB是⊙O的直徑，C點在⊙O上，AD平分角∠BAC交⊙O于D，過D作直線AC的垂線，交AC的延長線于E，連接BD，CD．
（1）求證：BD＝CD；
（2）求證：直線DE是⊙O的切線；
（3）若DE＝
，AB＝4，求AD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，AB=3，點M在CD的邊上，且DM=1，ΔAEM與ΔADM關于AM所在的直線對稱，將ΔADM按順時針方向繞點A旋轉90°得到ΔABF，連接EF，則線段EF的長為（ ）
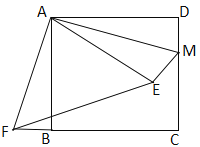
A. 3 B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
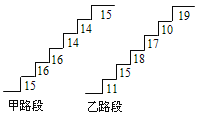
【題目】在某旅游景區上山的一條小路上，有一些斷斷續續的臺階，下圖是其中的甲、乙兩段臺階的示意圖，圖中的數字表示每一級臺階的高度（單位：cm）.請你用所學過的有關統計知識，回答下列問題（數據：15，16，16，14，14，15的方差
，數據：11，15，18，17，10，19的方差
：
（1）分別求甲、乙兩段臺階的高度平均數；
（2）哪段臺階走起來更舒服？與哪個數據（平均數、中位數、方差和極差）有關？
（3）為方便游客行走，需要陳欣整修上山的小路，對于這兩段臺階路.在總高度及臺階數不變的情況下，請你提出合理的整修建議.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了創建國家級衛生城區，某社區在九月份購買了甲、乙兩種綠色植物共1100盆，共花費了27000元．已知甲種綠色植物每盆20元，乙種綠色植物每盆30元．
（1）該社區九月份購買甲、乙兩種綠色植物各多少盆？
（2）十月份，該社區決定再次購買甲、兩種綠色植物．已知十月份甲種綠色植物每盆的價格比九月份的價格優惠
元
，十月份乙種綠色植物每盆的價格比九月份的價格優惠
．因創衛需要，該社區十月份購買甲種綠色植物的數量比九月份的數量增加了
，十為份購買乙種綠色植物的數量比九月份的數量增加了
．若該社區十月份的總花費與九月份的總花費恰好相同，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（感知）“如圖①，
，
平分
，作
，
、
分別交射線
、
于
、
兩點，連結
，求
的度數”為了求解問題，某同學做了如下的分析，
“過點
作
于點
，
于點
，”進而求解，則
________
．
（拓展）如圖②，一般地，設
，平分，作
，、分別交射線、于、兩點，連結．
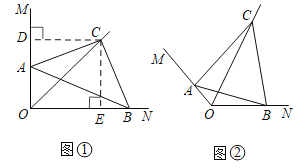
（1）求的度數．（用含
的代數式表示）
（2）若
，
，
，則
________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線
與
軸交于
，
兩點，與
軸交于點
，拋物線的對稱軸與軸交于點
，頂點坐標為
.
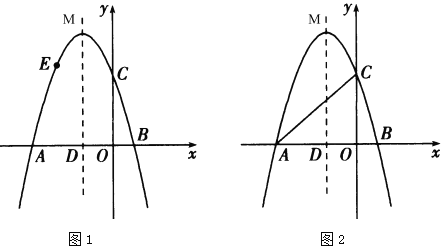
（1）求拋物線的表達式和頂點的坐標；
（2）如圖1，點
為拋物線上一點，點
不與點重合，當
時，過點作
軸，交拋物線的對稱軸于點
，作
軸于點H，得到矩形
，求矩形的周長的最大值；
（3）如圖2，點
為拋物線對稱軸上一點，是否存在點，使以點、
、為頂點的三角形是直角三角形？若存在，求出點的坐標；若不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
