
【題目】某種水果進價為每千克15元,銷售中發現,銷售單價定為20元時,日銷售量為50千克;當銷售單價每上漲1元,日銷售量就減少5千克.設銷售單價為![]() (元),每天的銷售量為
(元),每天的銷售量為![]() (千克),每天獲利為
(千克),每天獲利為![]() (元).
(元).
(1)求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)求![]() 與
與![]() 之間的函數關系式;該水果定價為每千克多少元時,每天的銷售利潤最大?最大利潤是多少元?
之間的函數關系式;該水果定價為每千克多少元時,每天的銷售利潤最大?最大利潤是多少元?
(3)如果商家規定這種水果每天的銷售量不低于40千克,求商家每天銷售利潤的最大值是多少元?
【答案】(1)![]() ;(2)該水果售價定為每千克23元時,每天的銷售利潤最大,最大利潤是245元;(3)商家每天銷售利潤的最大值是240元.
;(2)該水果售價定為每千克23元時,每天的銷售利潤最大,最大利潤是245元;(3)商家每天銷售利潤的最大值是240元.
【解析】
(1)根據“銷售單價每上漲1元,日銷售量就減少5千克”即可列出y與x之間的函數關系式;
(2)根據“利潤=每千克的利潤×銷售數量”即可列出w與x之間的函數關系式,將二次函數解析式轉化成頂點式即可得出答案;
(3)先根據銷售量求出自變量x的取值范圍,再根據二次函數的增減性進行解答即可.
解:(1)根據題意得:![]() ;
;
(2)根據題意得:![]() ,
,
![]() 與
與![]() 之間的函數關系式為:
之間的函數關系式為:
![]() ,
,
![]() ,
,
![]() 當
當![]() 時,
時,![]() 有最大值,最大值為245;
有最大值,最大值為245;
(3)由題意得:![]() ,
,
解得![]() .
.
![]() ,
,
![]() 當
當![]() 時,
時,![]() 有最大值,其最大值為
有最大值,其最大值為![]() (元).
(元).
答:商家每天銷售利潤的最大值是240元.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】甲、乙、丙、丁四位同學進行一次乒乓球單打比賽,要從中選出兩位同學打第一場比賽.
(1)請用樹狀圖法或列表法,求恰好選中甲、乙兩位同學的概率.
(2)若已確定甲打第一場,再從其余三位同學中隨機選取一位,求恰好選中乙同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
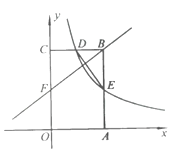
【題目】如圖,矩形OABC的頂點A,C分別在x軸和y軸上,點B的坐標為(2,3).雙曲線y=![]() (x>0)的圖象經過BC的中點D,且與AB交于點E,連接DE.
(x>0)的圖象經過BC的中點D,且與AB交于點E,連接DE.
(1)直接寫出k的值及點E的坐標;
(2)若點F是OC邊上一點,且FB⊥DE,求直線FB的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 的對稱軸為
的對稱軸為![]() ,與
,與![]() 軸的一個交點在
軸的一個交點在![]() 和
和![]() 之間,其部分圖像如圖所示,則下列結論:①點
之間,其部分圖像如圖所示,則下列結論:①點![]() ,
,![]() ,
,![]() 是該拋物線上的點,則
是該拋物線上的點,則![]() ;②
;②![]() ;③
;③![]() (
(![]() 為任意實數).其中正確結論的個數是( )
為任意實數).其中正確結論的個數是( )
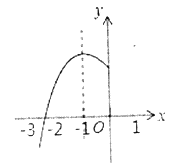
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的最大值為4,且該拋物線與
的最大值為4,且該拋物線與![]() 軸的交點為
軸的交點為![]() ,頂點為
,頂點為![]() .
.
(1)求該二次函數的解析式及點![]() ,
,![]() 的坐標;
的坐標;
(2)點![]() 是
是![]() 軸上的動點,
軸上的動點,
①求![]() 的最大值及對應的點
的最大值及對應的點![]() 的坐標;
的坐標;
②設![]() 是
是![]() 軸上的動點,若線段
軸上的動點,若線段![]() 與函數
與函數![]() 的圖像只有一個公共點,求
的圖像只有一個公共點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年5月20日是中國學生營養日,按時吃早餐是一種健康的飲食習慣,為了解本校九年級學生飲食習慣,某興趣小組在九年級隨機抽取了一部分學生每天吃早餐的情況,并將統計結果繪制成如下不完整的統計圖表:
組別 | 調查結果 | 所占百分比 |
A | 不吃早餐 | 25% |
B | 偶爾吃早餐 | 12.5% |
C | 經常吃早餐 | |
D | 每天吃早餐 | 50% |

請根據以上統計圖表,解答下列問題:
![]() 本次接受調查的總人數為_____人.
本次接受調查的總人數為_____人.
![]() 請補全條形統計圖.
請補全條形統計圖.
![]() 該校九年級共有學生
該校九年級共有學生![]() 人,請估計該校九年級學生每天吃早餐的人數;
人,請估計該校九年級學生每天吃早餐的人數;
![]() 請根據此次調查的結果提一條建議.
請根據此次調查的結果提一條建議.
查看答案和解析>>
科目:初中數學 來源: 題型:
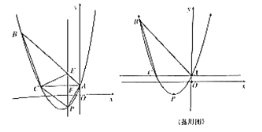
【題目】如圖,已知拋物線![]() (
(![]() >0)與
>0)與![]() 軸交于A,B兩點(A點在B點的左邊),與
軸交于A,B兩點(A點在B點的左邊),與![]() 軸交于點C。
軸交于點C。
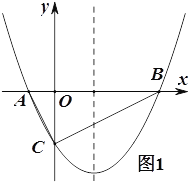
(1)如圖1,若△ABC為直角三角形,求![]() 的值;
的值;
(2)如圖1,在(1)的條件下,點P在拋物線上,點Q在拋物線的對稱軸上,若以BC為邊,以點B,C,P,Q為頂點的四邊形是平行四邊形,求P點的坐標;
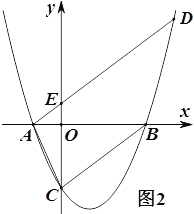
(3)如圖2,過點A作直線BC的平行線交拋物線于另一點D,交![]() 軸交于點E,若AE:ED=1:4,求
軸交于點E,若AE:ED=1:4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 經過
經過![]() 的三個頂點,其中點
的三個頂點,其中點![]() ,點
,點![]() ,
,![]() 軸,點
軸,點![]() 是直線
是直線![]() 下方拋物線上的動點.
下方拋物線上的動點.
(1)求拋物線的解析式;
(2)過點![]() 且與
且與![]() 軸平行的直線
軸平行的直線![]() 與直線
與直線![]() ,
,![]() 分別交于點
分別交于點![]() ,
,![]() ,當四邊形
,當四邊形![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標;
的坐標;
(3)當點![]() 為拋物線的頂點時,在直線
為拋物線的頂點時,在直線![]() 上是否存在點
上是否存在點![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,若存在,求出點
相似,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com