
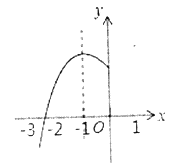
【題目】已知拋物線![]() 的對稱軸為
的對稱軸為![]() ,與
,與![]() 軸的一個交點在
軸的一個交點在![]() 和
和![]() 之間,其部分圖像如圖所示,則下列結論:①點
之間,其部分圖像如圖所示,則下列結論:①點![]() ,
,![]() ,
,![]() 是該拋物線上的點,則
是該拋物線上的點,則![]() ;②
;②![]() ;③
;③![]() (
(![]() 為任意實數).其中正確結論的個數是( )
為任意實數).其中正確結論的個數是( )
A. 0B. 1C. 2D. 3
【答案】C
【解析】
逐一分析3條結論是否正確:①根據拋物線的對稱性找出點(-![]() ,y3)在拋物線上,再結合拋物線對稱軸左邊的單調性即可得出①錯誤;②由x=-3時,y<0,即可得出9a-3b+c<0,根據拋物線的對稱軸為x=-1,即可得出b=2a,即可得出②正確;③∵拋物線開口向下,對稱軸為x=-1,有最大值
,y3)在拋物線上,再結合拋物線對稱軸左邊的單調性即可得出①錯誤;②由x=-3時,y<0,即可得出9a-3b+c<0,根據拋物線的對稱軸為x=-1,即可得出b=2a,即可得出②正確;③∵拋物線開口向下,對稱軸為x=-1,有最大值![]() ,再根據x=t時的函數值為at2+bt+c,由此即可得出③正確.綜上即可得出結論.
,再根據x=t時的函數值為at2+bt+c,由此即可得出③正確.綜上即可得出結論.
解:①∵拋物線的對稱軸為x=-1,點(![]() ,y3)在拋物線上,
,y3)在拋物線上,
∴(-![]() ,y3)在拋物線上.
,y3)在拋物線上.
∵-![]() <-
<-![]() <-
<-![]() ,且拋物線對稱軸左邊圖象y值隨x的增大而增大,
,且拋物線對稱軸左邊圖象y值隨x的增大而增大,
∴y1<y3<y2.∴①錯誤;
②∵拋物線y=ax2+bx+c(a≠0)的對稱軸為x=-1,
∴-![]() =-1,∴2a=b,∴a=
=-1,∴2a=b,∴a=![]()
∵當x=-3時,y=9a-3b+c<0,
∴9![]() -3b+c=
-3b+c=![]() <0,
<0,
∴3b+2c<0,∴②正確;
③∵拋物線y=ax2+bx+c(a≠0)的對稱軸為x=-1,開口向下
∴當x=-1,![]()
∵當x=t時,y= at2+bt+c
∵![]() 為任意實數
為任意實數
∴at2+bt+c≤![]()
∴at2+bt≤a-b.
∴③正確.
故選:C.


科目:初中數學 來源: 題型:
【題目】(本小題滿分8分)某廠制作甲、乙兩種環保包裝盒。已知同樣用6m的材料制成甲盒的個數比制成乙盒的個數少2個,且制成一個甲盒比制作一個乙盒需要多用20%的材料。
(1)求制作每個甲盒、乙盒各用多少材料?
(2)如果制作甲、乙兩種包裝盒3000個,且甲盒的數量不少于乙盒數量的2倍,那么請寫出所需材料總長度![]() 與甲盒數量
與甲盒數量![]() 之間的函數關系式,并求出最少需要多少米材料。
之間的函數關系式,并求出最少需要多少米材料。
查看答案和解析>>
科目:初中數學 來源: 題型:
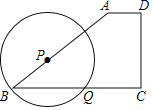
【題目】已知在梯形ABCD中,AD∥BC,AB=BC,DC⊥BC,且AD=1,DC=3,點P為邊AB上一動點,以P為圓心,BP為半徑的圓交邊BC于點Q.
(1)求AB的長;
(2)當BQ的長為![]() 時,請通過計算說明圓P與直線DC的位置關系.
時,請通過計算說明圓P與直線DC的位置關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,AB為⊙O的直徑,弦CD⊥AB于點E,在CD的延長線上取一點P,PG與⊙O相切于點G,連接AG交CD于點F.
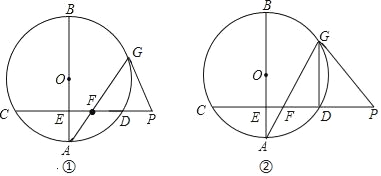
(Ⅰ)如圖①,若∠A=20°,求∠GFP和∠AGP的大小;
(Ⅱ)如圖②,若E為半徑OA的中點,DG∥AB,且OA=2![]() ,求PF的長.
,求PF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校計劃組織全校1441名師生到相關部門規劃的林區植樹,經過研究,決定租用當地租車公司一共62輛![]() 兩種型號客車作為交通工具.
兩種型號客車作為交通工具.
下表是租車公司提供給學校有關兩種型號客車的載客量和租金信息:
型號 | 載客量 | 租金單價 |
| 30人/輛 | 380元/輛 |
| 20人/輛 | 280元/輛 |
注:載客量指的是每輛客車最多可載該校師生的人數.設學校租用![]() 型號客車
型號客車![]() 輛,租車總費用為
輛,租車總費用為![]() 元.
元.
(1)求![]() 與
與![]() 的函數解析式,請直接寫出
的函數解析式,請直接寫出![]() 的取值范圍;
的取值范圍;
(2)若要使租車總費用不超過21940元,一共有幾種租車方案?哪種租車方案總費用最省?最省的總費用是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種水果進價為每千克15元,銷售中發現,銷售單價定為20元時,日銷售量為50千克;當銷售單價每上漲1元,日銷售量就減少5千克.設銷售單價為![]() (元),每天的銷售量為
(元),每天的銷售量為![]() (千克),每天獲利為
(千克),每天獲利為![]() (元).
(元).
(1)求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)求![]() 與
與![]() 之間的函數關系式;該水果定價為每千克多少元時,每天的銷售利潤最大?最大利潤是多少元?
之間的函數關系式;該水果定價為每千克多少元時,每天的銷售利潤最大?最大利潤是多少元?
(3)如果商家規定這種水果每天的銷售量不低于40千克,求商家每天銷售利潤的最大值是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
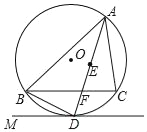
【題目】如圖,點E是△ABC的內心,AE的延長線交BC于點F,交△ABC的外接圓⊙O于點D,連接BD,過點D作直線DM,使∠BDM=∠DAC;
(1)求證:直線DM是⊙O的切線;
(2)若DF=2,AF=5,求BD長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com