
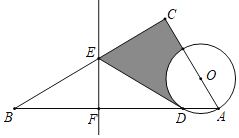
【題目】如圖,在△ABC中,∠C=90°,點O在AC上,以OA為半徑的⊙O交AB于點D,BD的垂直平分線交BC于點E,交BD于點F,連接DE.
(1)判斷直線DE與⊙O的位置關系,并說明理由;
(2)若∠B=30°,AC=6,OA=2,直接寫出陰影部分的面積.
【答案】(1)直線DE與⊙O相切;理由見解析;(2)![]() .
.
【解析】
(1)直線DE與⊙O相切,連接OD,由已知條件證明OD⊥DE即可證明DE是⊙O的切線;
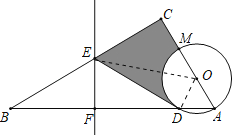
(2)連接OE,根據陰影部分的面積=四邊形CEDO-扇形DOM的面積計算即可.
(1)直線DE與⊙O相切,理由如下:
連接OD,
∵OD=OA,
∴∠A=∠ODA,
∵EF是BD的垂直平分線,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°﹣90°=90°,
即OD⊥DE,
又∵OD為⊙O的半徑,
∴直線DE與⊙O相切;
(2)連接OE,
∵∠B=30°,
∴∠A=60°,
∵OD=OA,
∴∠ODA=∠A=60°,
∴AD=AO=DO=2,∠MOD=120°,
∵AC=6,∠B=30°,
∴AB=12,
∴BD=10,
∵EF是BD的垂直平分線,
∴BF=DF=5,
∴EF=![]() ,BE=DE=
,BE=DE=![]() ,
,
∴CE=BC﹣BE=![]() ,
,
∴陰影部分的面積=四邊形CEDO﹣扇形DOM的面積=![]() ×
×![]() ×4+
×4+![]() ×
×![]() ×2﹣
×2﹣![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】中國高鐵近年來用震驚世界的速度不斷發展,已成為當代中國一張耀眼的“國家名片”。修建高鐵時常常要逢山開道、遇水搭橋。如圖,某高鐵在修建時需打通一直線隧道MN(M、N為山的兩側),工程人員為了計算MN兩點之間的直線距離,選擇了在測量點A、B、C進行測量,點B、C分別在AM、AN上,現測得AM=1200米,AN=2000米,AB=30米,BC=45米,AC=18米,求直線隧道MN的長。

查看答案和解析>>
科目:初中數學 來源: 題型:
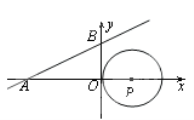
【題目】如圖,直線y=![]() x+
x+![]() 與x軸、y軸分別相交于A、B兩點,圓心P的坐標為(1,0),⊙P與y軸相切于點O.若將⊙P沿x軸向左移動,當⊙P與該直線相交時,滿足橫坐標為整數的點P的個數是( )
與x軸、y軸分別相交于A、B兩點,圓心P的坐標為(1,0),⊙P與y軸相切于點O.若將⊙P沿x軸向左移動,當⊙P與該直線相交時,滿足橫坐標為整數的點P的個數是( )
A.3B.4C.5D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠家一種摩托車如圖所示,它的大燈A射出的光線AB、AC與地面MN的夾角分別為8°和10°.
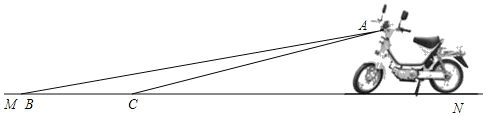
(1)該車大燈照亮地面的寬度BC是1.4m,求大燈A與地面距離約是多少?
(2)一般正常人從發現危險到做出剎車動作的反應時間是0.2s,從發現危險到摩托車完全停下所行駛的距離叫做最小安全距離,某人以60km/h的速度駕駛該車,突然遇到危險情況,立即剎車直到摩托車停止,在這個過程剎車距離是![]() m,請判斷(1)中的該車大燈A的地面高度是否能滿足最小安全距離的要去,若不能該如何調整A的高度?(參考數據:sin8°≈
m,請判斷(1)中的該車大燈A的地面高度是否能滿足最小安全距離的要去,若不能該如何調整A的高度?(參考數據:sin8°≈![]() ,tan8°≈
,tan8°≈![]() ,sin10°≈
,sin10°≈![]() ,tan10°≈
,tan10°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
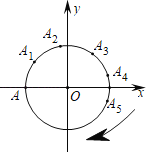
【題目】如圖,A點坐標是(﹣2,0),將點A繞原點O順時針旋轉40°,A的對應點是A1,將點A1繞原點O順時針旋轉40°,A1的對應點是A2,將點A2繞原點O順時針旋轉40°,A2的對應點是A3,…,按此規律Ai每次都繞原點O順時針旋轉40°得Ai+1,則A2019的坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,且
,且![]() ,頂點為
,頂點為![]() .
.
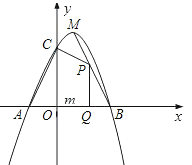
(1)求二次函數的解析式;
(2)點![]() 為線段
為線段![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 軸的垂線
軸的垂線![]() ,垂足為
,垂足為![]() ,若
,若![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 關于
關于![]() 的函數解析式,并寫出
的函數解析式,并寫出![]() 的取值范圍;
的取值范圍;
(3)探索:線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 為等腰三角形?如果存在,求出點
為等腰三角形?如果存在,求出點![]() 的坐標;如果不存在,請說呀理由.
的坐標;如果不存在,請說呀理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 的對稱軸為
的對稱軸為![]() ,與
,與![]() 軸的一個交點在
軸的一個交點在![]() 和
和![]() 之間,其部分圖象如圖所示,則下列結論:(1)
之間,其部分圖象如圖所示,則下列結論:(1)![]() :(2)
:(2)![]() ;(3)
;(3)![]() (
(![]() 為任意實數);(4)
為任意實數);(4)![]() ;5)點
;5)點![]()
![]()
![]() 是該拋物線上的點,且
是該拋物線上的點,且![]() ,其中正確結論的個數是( )
,其中正確結論的個數是( )
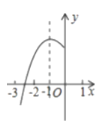
A. 2B. 3C. 4D. 5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com