
分析 (1)根據(jù)根與系數(shù)的關(guān)系,用含k的代數(shù)式表示出AB,、AC的和與積,利用AB2+AC2=(AB+AC)2-2AB•AC,由于第三邊的長(zhǎng)BC=5,得到關(guān)于k的方程,求出k的值;
(2)用含k的代數(shù)式表示出AB、AC,當(dāng)AB=5時(shí),求出△ABC的周長(zhǎng);當(dāng)AC=5時(shí),求出△ABC的周長(zhǎng).
解答 解:(1)∵AB、AC (AB≤AC)的長(zhǎng)是關(guān)于x的一元二次方程x2-(2k+1)x+k2+k=0的兩個(gè)實(shí)數(shù)根,
∴AB+AC=2k+1,AB•AC=k2+k
∴AB2+AC2=(AB+AC)2-2AB•AC
=[-(2k+1)]2-2(k2+k)
=4k2+4k+1-2k2-2k
=2k2+2k+1
若△ABC是以BC=5為斜邊的直角三角形,
∴AB2+AC2=52
即2k2+2k+1=25
∴k2+k-12=0
∴k1=3,k2=-4(不合題意,舍去)
即當(dāng)k=3時(shí),△ABC是以BC為斜邊的直角三角形.
(2)因?yàn)閤2-(2k+1)x+k2+k=0,
即(x-k-1)(x-k)=0
∴x1=k+1,x2=k
若k=5,所以k+1=6,此時(shí)l△ABC=5+5+6=16,
若k+1=5,所以k=4,此時(shí)l△ABC=5+5+4=14.
點(diǎn)評(píng) 本題主要考查了根與系數(shù)的關(guān)系、勾股定理、一元二次方程及等腰三角形的相關(guān)知識(shí).解決本題的關(guān)鍵是應(yīng)用完全平方公式的變形求出AB2+AC2.一元二次方程ax2+bx+c=0(a≠0)的根與系數(shù)的關(guān)系為:x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
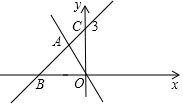 已知一次函數(shù)y=kx+b(k≠0)與y=kx(k≠0)的圖象交于A(-1,2),且與y軸分別交于B、C兩點(diǎn),若點(diǎn)C的縱坐標(biāo)為3,則△AOB的面積為3.
已知一次函數(shù)y=kx+b(k≠0)與y=kx(k≠0)的圖象交于A(-1,2),且與y軸分別交于B、C兩點(diǎn),若點(diǎn)C的縱坐標(biāo)為3,則△AOB的面積為3.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
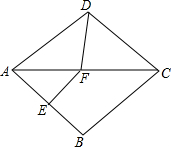 如圖,菱形ABCD中,∠B=100°,AB的垂直平分線交對(duì)角線AC于點(diǎn)F,E為垂足,連接DF,則∠CDF等于60°.
如圖,菱形ABCD中,∠B=100°,AB的垂直平分線交對(duì)角線AC于點(diǎn)F,E為垂足,連接DF,則∠CDF等于60°.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com