【題目】如圖，已知CE⊥AB，垂足為點E，DF⊥AB，垂足為點F，AF=BE，AC=BD，則下列結論：①Rt△AEC≌Rt△BFD；②∠C+∠B=90°；③AC∥BD；④∠A=∠D．
其中正確的結論為____．（填序號）
【答案】①②③
【解析】
由CE⊥AB，DF⊥AB可得△ACE和△BDF都是直角三角形；進而結合AC=BD，可以證明出△ACE≌△BDF；從上面的全等三角形可以得出其中相等的邊和角，即可以判斷題中正確的選項.
∵CE⊥AB，DF⊥AB
∴△ACE和△BDF都是直角三角形
∵AF=BE，EF公用
∴AE=BF
∵AE=BF，AC=BD，△ACE和△BDF都是直角三角形
∴Rt△AEC≌Rt△BFD
即①正確；
∵Rt△AEC≌Rt△BFD
∴∠CAB=∠ABD
故④錯誤；
∵在△AEC中，CE⊥AB
∴∠ACE+∠CAB=90°
∵∠ACE+∠CAB=90°，∠CAB=∠ABD
∴∠ACE+∠ABD=90°
故②正確；
∵∠CAB=∠ABD
∴AC∥BD
故③正確.
故答案為：①②③.
學練快車道快樂假期寒假作業系列答案
新思維寒假作業系列答案科目：初中數學 來源： 題型：
【題目】我們在學習“實數”時畫了這樣一個圖，即“以數軸上的單位長為‘1’的線段作一個正方形，然后以原點O為圓心，正方形的對角線長為半徑畫弧交數軸于點A”，請根據圖形回答下列問題：
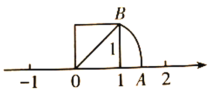
(1)線段OA的長度是多少?(要求寫出求解過程)
(2)這個圖形的目的是為了說明什么?
(3)這種研究和解決問題的方式體現了 的數學思想方法.(將下列符合的選項序號填在橫線上)
A.數形結合 B.代入 C.換元 D.歸納
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠C=90°，AD平分∠CAB，交CB于點D，過點D作DE⊥AB于點E．
（1）求證：△ACD≌△AED；
（2）若∠B=30°，CD=2，求BD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
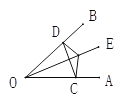
【題目】如圖，點E是∠AOB的平分線上一點，EC⊥OA，ED⊥OB，垂足分別為C、D．
求證：（1）∠ECD=∠EDC；
（2）OC=OD；
（3）OE是線段CD的垂直平分線．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是反比例函數y＝
的圖象的一個分支，對于給出的下列說法：
①常數k的取值范圍k>2；②另一分支在第三象限；③在函數圖象上取點A(a1，b1)和點B(a2，b2)，當a1>a2時，則b1<b2；④在函數圖象的某一分支上取點A(a1，b1)和點B(a2，b2)，當a1>a2時，則b1<b2.其中正確的是__________．(在橫線上填上正確的序號)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD的對角線相交于點O，AE平分∠BAD交BC于E， 若∠CAE=15°則∠BOE=（ ）
A. 30° B. 45° C. 60° D. 75°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】光明中學全體學生900人參加社會實踐活動，從中隨機抽取50人的社會實踐活動成績制成如圖所示的條形統計圖，結合圖中所給信息解答下列問題：
填寫下表：
中位數 | 眾數 | |
隨機抽取的50人的社會實踐活動成績 |
估計光明中學全體學生社會實踐活動成績的總分．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
