
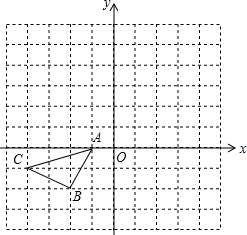
 在如圖所示的正方形格中,△ABC的頂點均在格點上請在所給直角坐標系中按要求畫圖和解答下列問題.
在如圖所示的正方形格中,△ABC的頂點均在格點上請在所給直角坐標系中按要求畫圖和解答下列問題.分析 (1)利用關于原點對稱的點的坐標特征寫出A1、B1、C1的坐標,然后描點即可得到△A1B1C1;
(2)利用網格特點和旋轉的性質畫出A、B、C的對應點A2、B2、C2,然后描點即可得到△A2B2C2,然后寫出B2的坐標,再利用弧長公式計算出點C經過的路徑長.
解答 解:(1)如圖,△A1B1C1為所作,點B1坐標為(2,2);
(2)如圖,△A2B2C2為所作,點B2的坐標為(2,-2),
AC=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
所以C經過的路徑長=$\frac{90•π•\sqrt{10}}{180}$=$\frac{\sqrt{17}}{2}$π.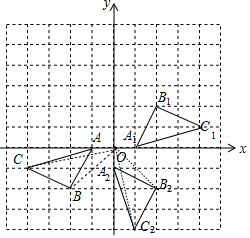
故答案為(2,2),(2,-2),$\frac{{\sqrt{17}}}{2}π$.
點評 本題考查了作圖-旋轉變換:根據旋轉的性質可知,對應角都相等都等于旋轉角,對應線段也相等,由此可以通過作相等的角,在角的邊上截取相等的線段的方法,找到對應點,順次連接得出旋轉后的圖形.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
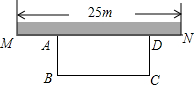 如圖,某中學準備在校園里利用圍墻的一段,再砌三面墻,圍成一個矩形花園ABCD(圍墻MN最長可利用25m),現在已備足可以砌50m長的墻的材料,
如圖,某中學準備在校園里利用圍墻的一段,再砌三面墻,圍成一個矩形花園ABCD(圍墻MN最長可利用25m),現在已備足可以砌50m長的墻的材料,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com