科目：初中數學 來源： 題型：
如圖，在?ABCD中，AB=6cm，AD=9cm，∠BAD的平分線交BC于點E，交DC的延長線于點F，BG⊥AE，垂足為G，BG=4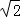
cm，則EF+CF的長為 ；
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
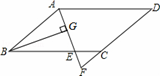
如圖，矩形ABCD中，O為AC中點，過點O的直線分別與AB，CD交于點E，F，連接BF交AC于點M，連接DE，BO．若∠COB=60°，FO=FC，則下列結論：
①FB⊥OC，OM=CM；
②△EOB≌△CMB；
③四邊形EBFD是菱形；
④MB：OE=3：2．
其中正確結論的個數是（ ）
|
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
查看答案和解析>>
科目：初中數學 來源： 題型：
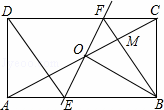
如圖，在等邊△ABC中，點D在直線BC上，連接AD，作∠ADN=60°，直線DN交射線AB于點E，過點C作CF∥AB交直線DN于點F．
（1）當點D在線段BC上，∠NDB為銳角時，如圖①，求證：CF+BE=CD；
（提示：過點F作FM∥BC交射線AB于點M．）
（2）當點D在線段BC的延長線上，∠NDB為銳角時，如圖②；當點D在線段CB的延長線上，∠NDB為鈍角時，如圖③，請分別寫出線段CF，BE，CD之間的數量關系，不需要證明；
（3）在（2）的條件下，若∠ADC=30°，S△ABC=4
，則BE= 8 ，CD= 4或8 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
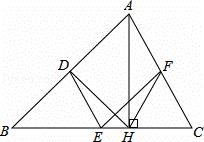
如圖，在△ABC中，點D，E，F分別是AB，BC，CA的中點，AH是邊BC上的高．
（1）求證：四邊形ADEF是平行四邊形；
（2）求證：∠DHF=∠DEF．
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，直角三角板ABC的斜邊AB＝12 cm，∠A＝30°，將三角板ABC繞C順時針旋轉90°至三角板A′B′C′的位置后，再沿CB方向向左平移，使點B′落在原三角板ABC的斜邊AB上，則三角板A′B′C′平移的距離為
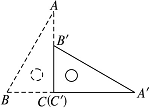
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
）÷
，其中x=cos60°．
÷
•
，
=﹣1/3．
（其中
），
時，求二次函數的對稱軸；
是△
的三邊長，當
時，二次函數最小值為
，試判斷△