
二次函數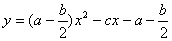 (其中
(其中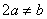 ),
),
(1)當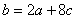 時,求二次函數的對稱軸;
時,求二次函數的對稱軸;
(2)若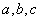 是△
是△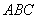 的三邊長,當
的三邊長,當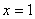 時,二次函數最小值為
時,二次函數最小值為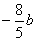 ,試判斷△
,試判斷△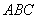 的形狀,并說明理由.
的形狀,并說明理由.
科目:初中數學 來源: 題型:
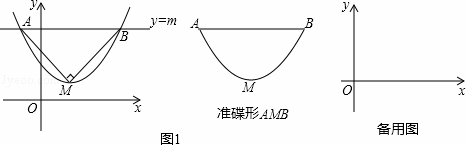
如圖1,拋物線y=ax2+bx+c(a>0)的頂點為M,直線y=m與x軸平行,且與拋物線交于點A,B,若△AMB為等腰直角三角形,我們把拋物線上A,B兩點之間的部分與線段AB圍成的圖形稱為該拋物線對應的準蝶形,線段AB稱為碟寬,頂點M稱為碟頂,點M到線段AB的距離稱為碟高.
(1)拋物線y=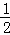 x2對應的碟寬
x2對應的碟寬 為 4 ;拋物線y=4x2對應的碟寬為
為 4 ;拋物線y=4x2對應的碟寬為 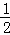 ;拋物線y=ax2(a>0)對應的碟寬為
;拋物線y=ax2(a>0)對應的碟寬為  ;拋物線y=a(x﹣2)2+3(a>0)對應的碟寬為
;拋物線y=a(x﹣2)2+3(a>0)對應的碟寬為  ;
;
(2)拋物線y=ax2﹣4ax﹣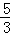 (a>0)對應的碟寬為6,且在x軸上,求a的值;
(a>0)對應的碟寬為6,且在x軸上,求a的值;
(3)將拋物線y=anx2+bnx+cn(an>0)的對應準蝶形記為Fn(n=1,2,3…),定義F1,F2,…,Fn為相似準蝶形,相應的碟寬之比即為相似比.若Fn與Fn﹣1的相似比為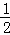 ,且Fn的碟頂是Fn﹣1的碟寬的中點,現將(2)中求得的拋物線記為y1,其對應的準蝶形記為F1.
,且Fn的碟頂是Fn﹣1的碟寬的中點,現將(2)中求得的拋物線記為y1,其對應的準蝶形記為F1.
①求拋物線y2的表達式;
②若F1的碟高為h1,F2的碟高為h2,…Fn的碟高為hn,則hn= ,Fn的碟寬有端點橫坐標為 ;F1,F2,…,Fn的碟寬右端點是否在一條直線上?若是,直接寫出該直線的表達式;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
某人帳戶現存款a元,每月支出b元,收入c元(a、b、c都是常數且大于0),則帳戶余額(不計利息)與月份的函數圖象可能是下圖中的( ).
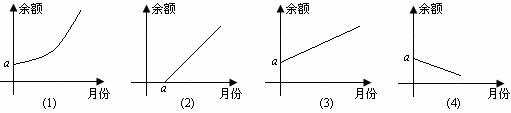
A.(1)(3) B.(3)(4) C.(1)(3)(4) D.(2)(3)(4)
查看答案和解析>>
科目:初中數學 來源: 題型:
浙江省居民生活用電可申請峰谷電,峰谷電價如下表:
| 高峰時間段用電價格表 | 低谷時間段用電價格表 | |
| 高峰電價 (單位:元/千瓦時) | 低谷月用電量 (單位:千瓦時) | 低谷電價 (單位:元/千瓦時) |
| 0.568 | 50及以下的部分 | 0.288 |
| 超過50至200的部分 | 0.318 | |
| 超過200的部分 | 0.388 |
小遠家5月份的高峰時間用電量為200千瓦時,低谷時間段用電量為300千瓦時,則按這種計費方式該家庭本月應付的電費為________元(精確到角).
查看答案和解析>>
科目:初中數學 來源: 題型:
將進貨單價為70元的某種商品按零售價100元/個售出時每天能賣出20個,若這種商品的零售價在一定范圍內每降價1元,其日銷售量就增加1個,為了獲得最大利潤,則應降價( )
A.4元 B.5元 C.8元 D.10元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com