【題目】設中學生體質健康綜合評定成績為
分，滿分為100分，規定：
為
級，
為
級，
為
級，
為
級.現隨機抽取某中學部分學生的綜合評定成績，整理繪制成如下兩幅不完整的統計圖，請根據圖中的信息，解答下列問題：
（1）在這次調查中，一共抽取了__________名學生；
（2）扇形統計圖中，
________%，級對應的圓心角為______度；
（3）若該中學共有學生1200名，請你利用你所學的統計知識，估計綜合評定成績為級的學生有多少名？
暑假銜接教材期末暑假預習武漢出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目：初中數學 來源： 題型：
【題目】已知x1，x2是關于x的一元二次方程x2－2(m＋1)x＋m2＋5＝0的兩實根．
(1)若(x1－1)(x2－1)＝28，求m的值；
(2)已知等腰△ABC的一邊長為7，若x1，x2恰好是△ABC另外兩邊的邊長，求這個三角形的周長．
【答案】（1）m的值為6;（2）17.
【解析】試題分析：
（1）由題意和根與系數的關系可得：x1＋x2＝2(m＋1)，x1x2＝m2＋5；由(x1－1)(x2－1)＝28，可得：x1x2－(x1＋x2)＝27；從而得到：m2＋5－2(m＋1)＝27，解方程求得m的值，再由“一元二次方程根的判別式”進行檢驗即可得到m的值；
（2）①當7為腰長時，則方程的兩根中有一根為7，代入方程可解得m的值（此時m的取值需滿足根的判別式△
），將m的值代入原方程，可求得兩根（此時兩根和7需滿足三角形三邊之間的關系），從而可求得等腰三角形的周長；
②當7為底邊時，則方程的兩根相等，由此可得“根的判別式△=0”，從而可得關于m的方程，解方程求得m的值，代入原方程可求得方程的兩根，再由三角形三邊之間的關系檢驗即可.
試題解析：
(1)(x1－1)(x2－1)＝28，即x1x2－(x1＋x2)＝27，而x1＋x2＝2(m＋1)，x1x2＝m2＋5，
∴m2＋5－2(m＋1)＝27，
解得m1＝6，m2＝－4，
又Δ＝[－2(m＋1)]2－4×1×(m2＋5)≥0時，m≥2，
∴m的值為6;
(2) 若7為腰長，則方程x2－2(m＋1)x＋m2＋5＝0的一根為7，
即72－2×7×(m＋1)＋m2＋5＝0，
解得m1＝10，m2＝4，
當m＝10時，方程x2－22x＋105＝0，根為x1＝15，x2＝7，不符合題意，舍去．
當m＝4時，方程為x2－10x＋21＝0，根為x1＝3，x2＝7，此時周長為7＋7＋3＝17
若7為底邊，則方程x2－2(m＋1)x＋m2＋5＝0有兩等根，
∴Δ＝0，解得m＝2，此時方程為x2－6x＋9＝0，根為x1＝3，x2＝3，3＋3<7，不成立，
綜上所述，三角形周長為17
點睛：（1）一元二次方程根與系數的關系成立的前提條件是方程要有實數根，即“根的判別式△
”；（2）涉及三角形邊長的問題中，解得的結果都需要用“三角形三邊之間的關系”檢驗，看三條線段能否圍成三角形.
【題型】解答題
【結束】
21
【題目】如圖，已知在△ABC中，D是AB的中點，且∠ACD=∠B，若 AB=10，求AC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
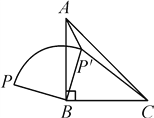
【題目】如圖，P是等腰直角△ABC外一點，把BP繞點B順時針旋轉90°到BP′，已知∠AP′B＝135°，P′A∶P′C＝1∶3，則P′A∶PB＝( )
A. 1∶
B. 1∶2 C. 
∶2 D. 1∶
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在讀書月活動中，學校準備購買一批課外讀物．為使課外讀物滿足同學們的需求，學校就“我最喜愛的課外讀物”從文學、藝術、科普和其他四個類別進行了抽樣調查（每位同學只選一類），如圖是根
據調查結果繪制的兩幅不完整的統計圖．
請你根據統計圖提供的信息，解答下列問題：
（1）本次調查中，一共調查了 名同學；
（2）條形統計圖中，m= ，n= ；
（3）扇形統計圖中，藝術類讀物所在扇形的圓心角是 度；
（4）學校計劃購買課外讀物6000冊，請根據樣本數據，估計學校購買其他類讀物多少冊比較合理？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示，對稱軸為直線
.下列結論中，正確的是（ ）
A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與探究
數學課上，老師讓同學們利用三角形紙片進行操作活動，探究有關線段之間的關系.
問題情境：
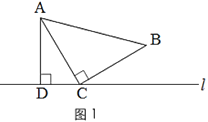
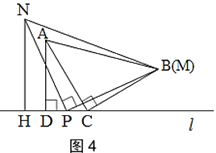
如圖1，三角形紙片ABC中，∠ACB＝90°，AC＝BC.將點C放在直線l上，點A，B位于直線l的同側，過點A作AD⊥l于點D.
初步探究：
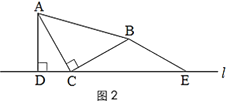
(1)在圖1的直線l上取點E，使BE＝BC，得到圖2.猜想線段CE與AD的數量關系，并說明理由；
變式拓展：
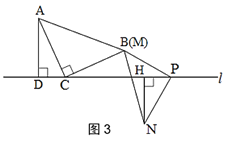
(2)小穎又拿了一張三角形紙片MPN繼續進行拼圖操作，其中∠MPN＝90°，MP＝NP.小穎在圖 1 的基礎上，將三角形紙片MPN的頂點P放在直線l上，點M與點B重合，過點N作NH⊥l于點 H.
請從下面 A，B 兩題中任選一題作答，我選擇_____題.
A.如圖3，當點N與點M在直線l的異側時，探究此時線段CP，AD，NH之間的數量關系，并說明理由.
B.如圖4，當點N與點M在直線l的同側，且點P在線段CD的中點時，探究此時線段CD，AD，NH之間的數量關系，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC 中，AD 是 BC 邊上的高，且∠ACB＝∠BAD，AE 平分∠CAD，交 BC于點 E，過點 E 作 EF∥AC，分別交 AB、AD 于點 F、G．則下列結論：①∠BAC＝90°；②∠AEF＝∠BEF； ③∠BAE＝∠BEA； ④∠B＝2∠AEF，其中正確的有（ ）
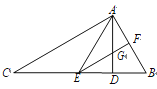
A. 4 個B. 3 個C. 2 個D. 1 個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
