
 如圖,已知在平面直角坐標(biāo)系中,點B在x軸上,半徑為3的⊙B與y軸相切,直線l過點A(-2,0),且和⊙B相切,與y軸相交于點C.若點E在直線l上,且以A為圓心,AE為半徑的圓與⊙B相切,求點E的坐標(biāo).
如圖,已知在平面直角坐標(biāo)系中,點B在x軸上,半徑為3的⊙B與y軸相切,直線l過點A(-2,0),且和⊙B相切,與y軸相交于點C.若點E在直線l上,且以A為圓心,AE為半徑的圓與⊙B相切,求點E的坐標(biāo). 分析 分兩種情形討論即可①當(dāng)⊙A與⊙B內(nèi)切時,直線l與⊙A交于點E1、E2,作E1M⊥x軸于M.設(shè)⊙B與直線l相切于點D,連接BD,則BD⊥直線l,則AE1=8.
②當(dāng)⊙A與⊙B外切時,⊙A與直線l交于點E2、E3,作E2N⊥x軸于N.則AE2=2,利用相似三角形的性質(zhì)分別求解即可.
解答 解:如圖,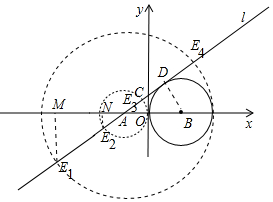
①當(dāng)⊙A與⊙B內(nèi)切時,直線l與⊙A交于點E1、E2,作E1M⊥x軸于M.設(shè)⊙B與直線l相切于點D,連接BD,則BD⊥直線l,
在RtADB中,AB=5,BD=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵⊙A與⊙B內(nèi)切,
∵AE1=8,
∵∠MAE1=∠DAB,∠E1MA=∠BDA,
∴△AME1∽△ADB,
∴$\frac{AM}{AD}$=$\frac{{E}_{1}M}{BD}$=$\frac{A{E}_{1}}{AB}$,
∴$\frac{AM}{4}$=$\frac{{E}_{1}M}{3}$=$\frac{8}{5}$,
∴AM=$\frac{32}{5}$,E1M=$\frac{24}{5}$,
∴OM=$\frac{42}{5}$,點E1(-$\frac{42}{5}$,-$\frac{24}{5}$),
∵E4與E1關(guān)于點A對稱,
∴E4($\frac{22}{5}$,-$\frac{24}{5}$).
②當(dāng)⊙A與⊙B外切時,⊙A與直線l交于點E2、E3,作E2N⊥x軸于N.則AE2=2,
由△ANE2∽△ADB,可得$\frac{AN}{AD}$=$\frac{N{E}_{2}}{BD}$=$\frac{A{E}_{2}}{AB}$,
∴$\frac{AN}{4}$=$\frac{N{E}_{2}}{3}$=$\frac{2}{5}$,
∴AN=$\frac{8}{5}$,NE2=$\frac{6}{5}$,ON=$\frac{18}{5}$,
∴E2(-$\frac{18}{5}$,-$\frac{6}{5}$).
∵E2與E3關(guān)于點A對稱,
∴E3(-$\frac{2}{5}$,$\frac{6}{5}$).
綜上所述,點E的坐標(biāo)為(-$\frac{42}{5}$,-$\frac{24}{5}$)或($\frac{22}{5}$,$\frac{24}{5}$)或(-$\frac{18}{5}$,-$\frac{6}{5}$)或(-$\frac{2}{5}$,$\frac{6}{5}$).
點評 本題考查切線的性質(zhì)、兩圓的位置關(guān)系、相似三角形的判定和性質(zhì)等知識,解題的關(guān)鍵是學(xué)會用分類討論的思想思考問題,屬于中考常考題型.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:初中數(shù)學(xué) 來源: 題型:選擇題
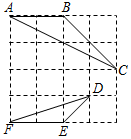 如圖,在4×4的正方形方格中,△ABC和△DEF的頂點都在邊長為1的小正方形頂點上,則tan∠ACB的值為( )
如圖,在4×4的正方形方格中,△ABC和△DEF的頂點都在邊長為1的小正方形頂點上,則tan∠ACB的值為( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
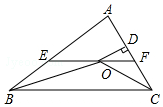 如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點O,過點O作EF∥BC交AB于E,交AC于F,過點O作OD⊥AC于D,下列四個結(jié)論:
如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點O,過點O作EF∥BC交AB于E,交AC于F,過點O作OD⊥AC于D,下列四個結(jié)論:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
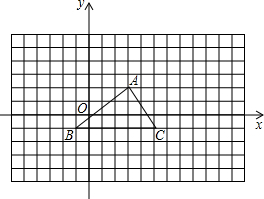 如圖所示的網(wǎng)格中,每個小方格都是邊長為1的正方形,B點的坐標(biāo)為(-1,-1).
如圖所示的網(wǎng)格中,每個小方格都是邊長為1的正方形,B點的坐標(biāo)為(-1,-1).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com