
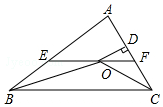
 如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點O,過點O作EF∥BC交AB于E,交AC于F,過點O作OD⊥AC于D,下列四個結論:
如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點O,過點O作EF∥BC交AB于E,交AC于F,過點O作OD⊥AC于D,下列四個結論:分析 由在△ABC中,∠ABC和∠ACB的平分線相交于點O,根據角平分線的定義與三角形內角和定理,即可求得②∠BOC=90°+$\frac{1}{2}$∠A正確;由平行線的性質和角平分線的定義得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正確;由角平分線的性質得出點O到△ABC各邊的距離相等,故③正確;由角平分線定理與三角形面積的求解方法,即可求得③設OD=m,AE+AF=n,則S△AEF=$\frac{1}{2}$mn,故④錯誤.
解答 解:∵在△ABC中,∠ABC和∠ACB的平分線相交于點O,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°-$\frac{1}{2}$∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=90°+$\frac{1}{2}$∠A;故②正確;
∵在△ABC中,∠ABC和∠ACB的平分線相交于點O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正確;
過點O作OM⊥AB于M,作ON⊥BC于N,連接OA,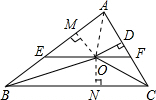
∵在△ABC中,∠ABC和∠ACB的平分線相交于點O,
∴ON=OD=OM=m,$\frac{1}{2}$∴S△AEF=S△AOE+S△AOF=$\frac{1}{2}$AE•OM+$\frac{1}{2}$AF•OD=$\frac{1}{2}$OD•(AE+AF)=$\frac{1}{2}$mn;故④錯誤;
∵在△ABC中,∠ABC和∠ACB的平分線相交于點O,
∴點O到△ABC各邊的距離相等,故③正確.
故答案是:①②③
點評 此題考查了角平分線的定義與性質,等腰三角形的判定與性質.此題難度適中,解題的關鍵是注意數形結合思想的應用.


科目:初中數學 來源: 題型:解答題
| 事件A | 必然事件 | 隨機事件 |
| m的值 | 3 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知在平面直角坐標系中,點B在x軸上,半徑為3的⊙B與y軸相切,直線l過點A(-2,0),且和⊙B相切,與y軸相交于點C.若點E在直線l上,且以A為圓心,AE為半徑的圓與⊙B相切,求點E的坐標.
如圖,已知在平面直角坐標系中,點B在x軸上,半徑為3的⊙B與y軸相切,直線l過點A(-2,0),且和⊙B相切,與y軸相交于點C.若點E在直線l上,且以A為圓心,AE為半徑的圓與⊙B相切,求點E的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
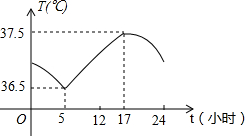 正常人的體溫一般在37℃左右,但一天中的不同時刻不盡相同圖反映了一天24小時內小明體溫的變化情況,下列說法錯誤的是( )
正常人的體溫一般在37℃左右,但一天中的不同時刻不盡相同圖反映了一天24小時內小明體溫的變化情況,下列說法錯誤的是( )| A. | 清晨5時體溫最低 | |
| B. | 下午5時體溫最高 | |
| C. | 從5時至24時,小明體溫一直是升高的 | |
| D. | 從0時至5時,小明體溫一直是下降的 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0 | B. | $\sqrt{5}$ | C. | $\frac{2}{7}$ | D. | -4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com