
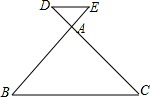
 如圖所示,已知:
如圖所示,已知: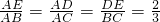 ,則
,則 =________,
=________,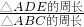 =________;若AD=2cm,則CD=________cm;若BE=10cm,則AB=________cm;若△ABC的周長是15cm,則△ADE的周長=________cm.
=________;若AD=2cm,則CD=________cm;若BE=10cm,則AB=________cm;若△ABC的周長是15cm,則△ADE的周長=________cm.
 5 6 10
5 6 10 AC,所以易求
AC,所以易求 =
= ;根據相似三角形的判定定理(對應邊成比例,兩個三角形相似)可知,
;根據相似三角形的判定定理(對應邊成比例,兩個三角形相似)可知,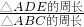 ,從而知△ADE的周長.
,從而知△ADE的周長. =
= =
= =
= ,
, AC,
AC, AC,
AC, =
= ;
;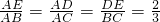 ,
,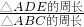 =
= (相似三角形的周長的比等于相似比);
(相似三角形的周長的比等于相似比); ×15=10(cm).
×15=10(cm). ;
; ;5;6;10.
;5;6;10.

科目:初中數學 來源:2011年九年級學業考試數學科適應性測試卷(解析版) 題型:填空題
 ,則
,則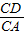 = ,
= , = ;若AD=2cm,則CD= cm;若BE=10cm,則AB= cm;若△ABC的周長是15cm,則△ADE的周長= cm.
= ;若AD=2cm,則CD= cm;若BE=10cm,則AB= cm;若△ABC的周長是15cm,則△ADE的周長= cm.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com