
如圖,在平面直角坐標系中,坐標原點為O,A點坐標為(4,0),B點坐標為(﹣1,0),以AB的中點P為圓心,AB為直徑作⊙P的正半軸交于點C.
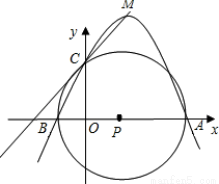
(1)求經過A、B、C三點的拋物線所對應的函數解析式;
(2)設M為(1)中拋物線的頂點,求直線MC對應的函數解析式;
(3)試說明直線MC與⊙P的位置關系,并證明你的結論.
(1)y=-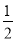 x2+
x2+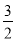 x+2,(2)
x+2,(2)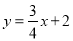 .(3)MC與⊙P的位置關系是相切.證明見解析.
.(3)MC與⊙P的位置關系是相切.證明見解析.
【解析】
試題分析:(1)求出半徑,根據勾股定理求出C的坐標,設經過A、B、C三點拋物線解析式是y=a(x-4)(x+1),把C(0,2)代入求出a即可;
(2)求出M的坐標,設直線MC對應函數表達式是y=kx+b,把C(0,2),M(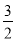 ,
,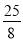 )代入得到方程組,求出方程組的解即可;
)代入得到方程組,求出方程組的解即可;
(3)根據點的坐標和勾股定理分別求出PC、DC、PD的平方,根據勾股定理的逆定理得出∠PCD=90°,即可求出答案.
試題解析:(1)連接PC,
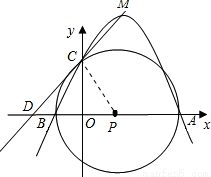
∵A(4,0),B(-1,0),
∴AB=5,半徑PC=PB=PA=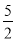 ,
,
∴OP=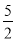 -1=
-1=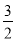 ,
,
在△CPO中,由勾股定理得:OC=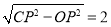
∴C(0,2),
設經過A、B、C三點拋物線解析式是y=a(x-4)(x+1),
把C(0,2)代入得:2=a(0-4)(0+1),
∴a=-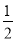 ,
,
∴y=-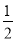 (x-4)(x+1)=-
(x-4)(x+1)=-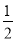 x2+
x2+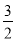 x+2,
x+2,
(2)y=-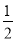 x2+
x2+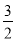 x+2=-
x+2=-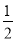 (x-
(x-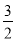 )2+
)2+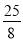 ,
,
M(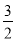 ,
,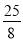 ),
),
設直線MC對應函數表達式是y=kx+b,
把C(0,2),M(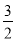 ,
,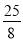 )代入得:
)代入得:

解得: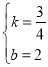 ,
,
∴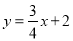 .
.
(3)MC與⊙P的位置關系是相切.
證明:設直線MC交x軸于D,
當y=0時,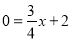 ,
,
∴x=-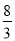 ,OD=
,OD=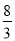 ,
,
∴D(-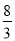 ,0),
,0),
在△COD中,由勾股定理得:CD2=22+(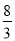 )2=
)2=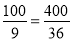 ,
,
PC2=(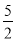 )2=
)2=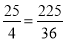 ,
,
PD2=(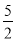 +
+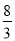 -1)2=
-1)2=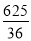 ,
,
∴CD2+PC2=PD2,
∴∠PCD=90°,
∴PC⊥DC,
∵PC為半徑,
∴MC與⊙P的位置關系是相切.
考點:二次函數綜合題


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案科目:初中數學 來源:2014-2015學年四川省仁壽縣聯誼學校九年級上學期期中考試數學試卷(解析版) 題型:解答題
如圖,在矩形ABCD中,AB=15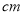 ,BC=10
,BC=10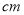 ,點P沿AB邊從點A開始向B點以
,點P沿AB邊從點A開始向B點以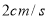 的速度移動,點Q沿DA邊從點D開始向點A以
的速度移動,點Q沿DA邊從點D開始向點A以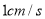 的速度移動。若P、 Q同時出發,用t(秒)表示移動時間。
的速度移動。若P、 Q同時出發,用t(秒)表示移動時間。

(1)問:當t=5時,求Δ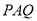 的面積是多少?
的面積是多少?
(2)當t為何值時,Δ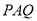 為等腰直角三角形?
為等腰直角三角形?
(3)當t為何值時,以點P、A、Q為頂點的 Δ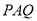 與Δ
與Δ 相似?
相似?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省仁壽縣聯誼學校九年級上學期期中考試數學試卷(解析版) 題型:選擇題
如圖,在ΔABC中,DE//BC,AQ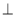 BC于Q,交DE于P,AD=3,BD=2,則
BC于Q,交DE于P,AD=3,BD=2,則 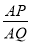 等于( )
等于( )

A.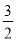 B.
B.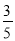 C.
C.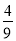 D.
D.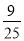
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江西省九年級上學期第二次月考數學試卷(解析版) 題型:解答題
如圖,在矩形ABCD中,E,F為BC上兩點,且BE=CF,連接AF,DE交于點O.求證:
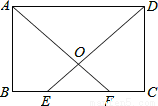
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江西省九年級上學期第二次月考數學試卷(解析版) 題型:填空題
小明從圖所示的二次函數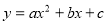 的圖象中,觀察得出了下面五條信息:①
的圖象中,觀察得出了下面五條信息:①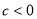 ;②
;②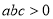 ;③
;③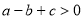 ;④
;④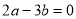 ;⑤
;⑤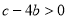 ,你認為其中正確信息有 。
,你認為其中正確信息有 。
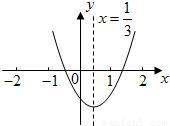
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級12月月考數學試卷(解析版) 題型:解答題
為了倡導“節約用水,從我做起”,市政府決定對市直機關500戶家庭的用水情況作一次調查,市政府調查小組隨機抽查了其中的100戶家庭一年的月平均用水量(單位:噸),并將調查結果制成了如圖所示的條形統計圖.

(1)請將條形統計圖補充完整;
(2)求這100個樣本數據的平均數,眾數和中位數;
(3)根據樣本數據,估計市直機關500戶家庭中月平均用水量不超過12噸的約有多少戶?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省咸寧市中考模擬考試數學試卷(解析版) 題型:選擇題
函數y= 的自變量x的取值范圍是( )
的自變量x的取值范圍是( )
A.x≠4 B.x>4 C.x≥4 D.x≤4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com