⊙O的半徑為6，⊙O的一條弦長4
，以4為半徑的同心圓與此弦的位置關系是（ ）
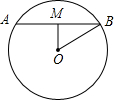
如圖，已知：AB=4
，OB=6，
∵M為AB中點，
∴AM=BM=2
，
根據(jù)勾股定理可知：OM=
=
=
=4，
∴以4為半徑的同心圓與此弦的位置關系是：相切．
故選C．
練習冊系列答案
相關習題
科目：初中數(shù)學
來源：不詳
題型：解答題
如圖，在△ABC中，AB=AC，以AB為直徑的⊙O交BC于點D，DE⊥AC，垂足為點E．
（1）求證：直線DE與⊙O相切；
（2）當AB=9，BC=6時，求線段DE的長．
查看答案和解析>>
科目：初中數(shù)學
來源：不詳
題型：填空題
在Rt△ABC中，∠C=90°，BC=5，AC=12，若以C為圓心，R為半徑作的圓與斜邊AB沒有公共點，則R的取值范圍是______．
查看答案和解析>>
科目：初中數(shù)學
來源：不詳
題型：單選題
如圖，AB是⊙O的直徑，BC交⊙O于點D，DE⊥AC于點E，要使DE是⊙O的切線，還需補充一個條件，則補充的條件不正確的是（ ）
| A．DE=DO | B．AB=AC | C．CD=DB | D．AC∥OD |
查看答案和解析>>
科目：初中數(shù)學
來源：不詳
題型：解答題
如圖，已知AB是⊙O的直徑，點C在⊙O上，過點C的直線與AB的延長線交于點P，AC=PC，∠CO
B=2∠PCB．
（1）求證：PC是⊙O的切線；
（2）求∠P的度數(shù)；
（3）點M是弧AB的中點，CM交AB于點N，AB=4，求線段BM、CM及弧BC所圍成的圖形面積．
查看答案和解析>>
科目：初中數(shù)學
來源：不詳
題型：填空題
如圖，P是⊙O的直徑CB延長線上的一點，PA是⊙O的切線，切點為A，∠P=20°，則∠ABP=______度．
查看答案和解析>>
科目：初中數(shù)學
來源：不詳
題型：解答題
已知⊙O過點D（4，3），點H與點D關于y軸對稱，過H作⊙O的切線交y軸于點A（如圖1）．
（1）求⊙O半徑；
（2）sin∠HAO的值；
（3）如圖2，設⊙O與y軸正半軸交點P，點E、F是線段OP上的動點（與P點不重合），連接并延長DE，DF交⊙O于點B，C，直線BC交y軸于點G，若△DEF是以EF為底的等腰三角形，試探索sin∠CGO的大小怎樣變化？請說明理由．
查看答案和解析>>
科目：初中數(shù)學
來源：不詳
題型：解答題
如圖，在Rt△ABC中，∠C=90°，O、D分別為AB、BC上的點．經(jīng)過A、D兩點的⊙O分別交
AB、AC于點E、F，且D為
 |
| EF |
的中點．
（1）求證：BC與⊙O相切；
（2）當AD=
2，∠CAD=30°時．求
|
| AD |
的長．
查看答案和解析>>
科目：初中數(shù)學
來源：不詳
題型：填空題
如圖．若△ABC的BC邊上的高為AH，BC長為30cm，DE
∥BC，以DE為直徑的半圓與BC切于F，若此半圓的面積是18πcm
2，則AH=______cm．
查看答案和解析>>
