
【題目】已知如圖![]() ,在以
,在以![]() 為原點的平面直角坐標系中,拋物線
為原點的平面直角坐標系中,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,
,![]() ,直線
,直線![]() 過點
過點![]() 且平行于
且平行于![]() 軸,
軸,![]() ,
,
![]() 求拋物線對應的二次函數的解析式;
求拋物線對應的二次函數的解析式;
![]() 若
若![]() 為拋物線
為拋物線![]() 上一動點,是否存在直線
上一動點,是否存在直線![]() 使得點
使得點![]() 到直線
到直線![]() 的距離與
的距離與![]() 的長恒相等?若存在,求出此時
的長恒相等?若存在,求出此時![]() 的值;
的值;
![]() 如圖
如圖![]() ,若
,若![]() 、
、![]() 為上述拋物線上的兩個動點,且
為上述拋物線上的兩個動點,且![]() ,線段
,線段![]() 的中點為
的中點為![]() ,求點
,求點![]() 縱坐標的最小值.
縱坐標的最小值.

【答案】(1)![]() ;(2)見解析;(3)2.
;(2)見解析;(3)2.
【解析】
(1)根據點C坐標,可得c=-1,然后根據AO=2CO,可得出點A坐標,將點A坐標代入求出b值,即可得出函數解析式;
(2)假設存在直線l使得點D到直線l的距離與OD的長恒相等,設出點D坐標,分別求出OD和點D到直線l的距離,然后列出等式求出t的值;
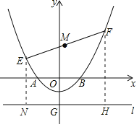
(3)作EN⊥直線l于點G,FH⊥直線l于點H,設出點E、F坐標,表示出點M的縱坐標,根據(2)中得出的結果,代入結果求出M縱坐標的最小值.
![]() ∵
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴點![]() 坐標為
坐標為![]() ,
,
代入得:![]() ,
,
解得:![]() ,
,
∴解析式為:![]() ;
;
![]() 假設存在直線
假設存在直線![]() 使得點
使得點![]() 到直線
到直線![]() 的距離與
的距離與![]() 的長恒相等,
的長恒相等,
設![]() ,
,
則![]() ,
,
點![]() 到直線
到直線![]() 的距離:
的距離:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
故當![]() 時,直線
時,直線![]() 使得點
使得點![]() 到直線
到直線![]() 的距離與
的距離與![]() 的長恒相等;
的長恒相等;
![]() 作
作![]() 直線
直線![]() 于點
于點![]() ,
,![]() 直線
直線![]() 于點
于點![]() ,
,
設![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,
∵![]() 為
為![]() 中點,
中點,
∴![]() 縱坐標為:
縱坐標為:![]() ,
,
由![]() 得:
得:![]() ,
,![]() ,
,
∴![]() ,
,
要使![]() 縱坐標最小,即
縱坐標最小,即![]() 最小,
最小,
當![]() 過點
過點![]() 時,
時,![]() 最小,最小值為
最小,最小值為![]() ,
,
∴![]() 縱坐標最小值為
縱坐標最小值為![]() .
.


科目:初中數學 來源: 題型:
【題目】某學校開展“書香校園”活動以來,受到同學們的廣泛關注,學校為了解全校學生課外閱讀的情況,隨機調查了部分學生在一周內借閱圖書的次數,并制作了不完整的統計圖表.
學生借閱圖書的次數統計表
借閱圖書的次數 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人數 | 6 | 15 | a | 12 | 9 |
學生借閱圖書的次數扇形統計圖

請你根據統計圖表中的信息,解答下列問題:
(1)a= ,b= ;
(2)該樣本數據的中位數是 次,眾數是 次;
(3)請計算扇形統計圖中“3次”所對應的扇形圓心角的度數;
(4)若該校共有2400名學生,根據調查結果,估計該校學生在一周內借閱圖書“4次及以上”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線l:y=x,過點A1(1,0)作x軸的垂線交直線l于點B1,以A1B1為邊作正方形A1B1C1A2,過點A2作x軸的垂線交直線l于點B2,以A2B2為邊作正方形A2B2C2A3,…;則點A5的坐標為_____,點Cn的坐標為_____.
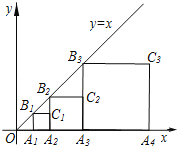
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了防止水土流失,某村開展綠化荒山活動,計劃經過若干年使本村綠化總面積新增360萬平方米.自2014年初開始實施后,實際每年綠化面積是原計劃的1.6倍,這樣可提前4年完成任務.問實際每年綠化面積多少萬平方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】湖南師大附中組織集團校內七、八、九年級學生參加“12KM”作文比賽,該校將收到的參賽作文進行分年級統計,繪制了如圖1和如圖2兩幅不完整的統計圖,根據圖中提供的信息完成以下問題.
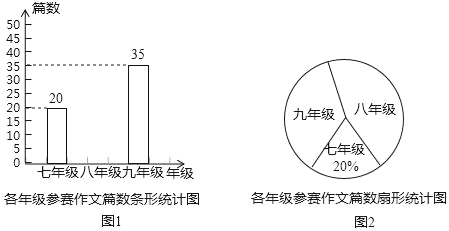
(1)扇形統計圖中九年級參賽作文篇數對應的圓心角是 度.八年級參賽作文篇數對應的百分比是 .
(2)請補全條形統計圖.
(3)經過評審,全集團校內有4篇作文榮獲特等獎,其中一篇來自九年級,學校準備從特等獎作文中任選兩篇刊登在校報上,請利用畫樹狀圖或列表的方法求出九年級特等獎作文被選登在校報上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
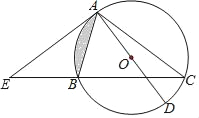
【題目】如圖,△ABC內接于⊙O,AD是⊙O直徑,E是CB延長線上一點,且∠BAE=∠C.
(1)求證:直線AE是⊙O的切線;
(2)若∠BAE=30°,⊙O的半徑為2,求陰影部分的面積;
(3)若EB=AB,cos∠E=![]() ,AE=24,求EB的長及⊙O的半徑.
,AE=24,求EB的長及⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示是兩張形狀、大小相同但是畫面不同的圖片,把兩張圖片從中間剪斷,再把四張形狀相同的小圖片(標注a、b、c、d)混合在一起,從四張圖片中隨機摸取一張,接著再隨機摸取一張,則這兩張小圖片恰好合成一張完整圖片的概率是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 在
在![]() 的正北方向,
的正北方向,![]() 在
在![]() 的正東方向,且
的正東方向,且![]() .某一時刻,甲車從
.某一時刻,甲車從![]() 出發,以
出發,以![]() 的速度朝正東方向行駛,與此同時,乙車從
的速度朝正東方向行駛,與此同時,乙車從![]() 出發,以
出發,以![]() 的速度朝正北方向行駛.
的速度朝正北方向行駛.![]() 小時后,位于點
小時后,位于點![]() 處的觀察員發現甲、乙兩車之間的夾角為
處的觀察員發現甲、乙兩車之間的夾角為![]() ,即
,即![]() ,此時,甲、乙兩人相距的距離為( )
,此時,甲、乙兩人相距的距離為( )
A. 90km B. 50![]() km C. 20
km C. 20![]() km D. 100km
km D. 100km
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com