
| A. | 1 | B. | 5 | C. | 1或5 | D. | 2或4 |
分析 由點C是劣弧$\widehat{AB}$的中點,得到OC垂直平分AB,求得DA=DB=3,根據勾股定理得到OD=$\sqrt{{5}^{2}-{3}^{2}}$=1,若△POC為直角三角形,只能是∠OPC=90°,則根據相似三角形的性質得到PD=2,于是得到結論.
解答 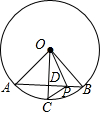 解:∵點C是劣弧$\widehat{AB}$的中點,
解:∵點C是劣弧$\widehat{AB}$的中點,
∴OC垂直平分AB,
∴DA=DB=3,
∴OD=$\sqrt{{5}^{2}-{3}^{2}}$=4,
若△POC為直角三角形,只能是∠OPC=90°,
則△POD∽△CPD,
∴$\frac{PD}{OD}=\frac{CD}{PD}$,
∴PD2=4×1=4,
∴PD=2,
∴PB=3-2=1,
根據對稱性得,
當P在OC的左側時,PB=3+2=5,
∴PB的長度為1或5,
故選C.
點評 本題考查了圓周角,弧,弦的關系,勾股定理,垂徑定理,正確左側圖形是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
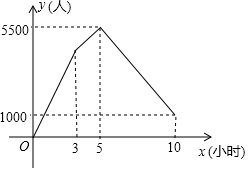 國家“5A”級景區某日迎來客流高峰,從索道開始運行前3小時開始,每小時都有a名游客源源不斷地涌入候客大廳排隊.索道每小時運送b名游客上山,索道運行2小時后,景區調來若干輛汽車和索道一起送游客上山,其中每小時有$\frac{7}{5}$b名游客乘坐汽車上山.5小時后,在候客大廳排隊的游客人數降至1000人,候客大廳排隊的游客人數y(人)與游客開始排隊后的時間x(小時)之間的關系如圖所示.則a=1500.
國家“5A”級景區某日迎來客流高峰,從索道開始運行前3小時開始,每小時都有a名游客源源不斷地涌入候客大廳排隊.索道每小時運送b名游客上山,索道運行2小時后,景區調來若干輛汽車和索道一起送游客上山,其中每小時有$\frac{7}{5}$b名游客乘坐汽車上山.5小時后,在候客大廳排隊的游客人數降至1000人,候客大廳排隊的游客人數y(人)與游客開始排隊后的時間x(小時)之間的關系如圖所示.則a=1500.查看答案和解析>>
科目:初中數學 來源:2017屆浙江省九年級3月模擬數學試卷(解析版) 題型:判斷題
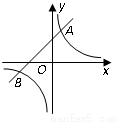
如圖,反比例函數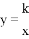 的圖象與一次函數
的圖象與一次函數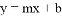 的圖象交于
的圖象交于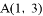 ,
,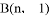 兩點.
兩點.
(1)求反比例函數與一次函數的解析式;
(2)根據圖象回答:當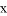 取何值時,反比例函數的值大于一次函數的值.
取何值時,反比例函數的值大于一次函數的值.
查看答案和解析>>
科目:初中數學 來源:2017屆山東省文慧學校九年級下學期第一次月考數學試卷(解析版) 題型:單選題
如圖,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分線,DE交AB于點D,連接CD,則CD=( )
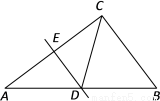
A. 3 B. 4 C. 4.8 D. 5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com