
【題目】對于平面中給定的一個圖形及一點 P,若圖形上存在兩個點 A、B,使得△PAB 是邊長為 2 的等邊三角形,則稱點 P 是該圖形的一個“美好點”.
(1)若將 x 軸記作直線 l,下列函數的圖象上存在直線 l 的“美好點”的是 (只填選項)
A.正比例函數 y x
B.反比例函數 y ![]()
C.二次函數 y x![]() 2
2
(2)在平面直角坐標系 xOy 中,若點 M (![]() n, 0) , N (0, n) ,其中n0 ,⊙O 的半徑為 r.
n, 0) , N (0, n) ,其中n0 ,⊙O 的半徑為 r.
①若r 2![]() ,⊙O 上恰好存在 2 個直線 MN 的“美好點”,求 n 的取值范圍;
,⊙O 上恰好存在 2 個直線 MN 的“美好點”,求 n 的取值范圍;
②若n4 ,線段 MN 上存在⊙O 的“美好點”,直接寫出 r 的取值范圍.
【答案】(1)A,B (2)①2<![]() <6,②
<6,②![]() .
.
【解析】
(1)把每個函數的圖像畫好,利用美好點的定義畫出符合條件的等邊![]() 直接可以作出判斷.
直接可以作出判斷.
(2)①弄懂題意,將直線MN沿![]() 軸平移,利用空間想象能力找到一個美好點時,三個美好點時的模型,然后利用不等式組求得
軸平移,利用空間想象能力找到一個美好點時,三個美好點時的模型,然后利用不等式組求得![]() 的范圍.
的范圍.
②沿①問的思路直接列出不等式求解.
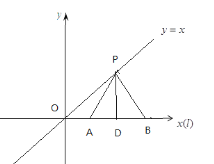
解:(1)如下圖:P是直線![]() 的美好點,則
的美好點,則![]() 是邊長為2的等邊三角形,所以
是邊長為2的等邊三角形,所以![]() ,過P作
,過P作![]() 垂足為D,則
垂足為D,則![]() 又P是直線
又P是直線![]() 上的點,所以
上的點,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 上存在
上存在![]() 的美好點.故A正確.
的美好點.故A正確.
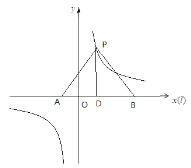
如下圖:P是直線![]() 的美好點,則
的美好點,則![]() 是邊長為2的等邊三角形,所以
是邊長為2的等邊三角形,所以![]() ,過P作
,過P作![]() 垂足為D,則
垂足為D,則![]() 又P是直線
又P是直線![]() 上的點,所以P的縱坐標是
上的點,所以P的縱坐標是![]() ,把縱坐標代入函數解析式的橫坐標為
,把縱坐標代入函數解析式的橫坐標為![]() 所以
所以![]() ,所以
,所以![]() 上存在
上存在![]() 的美好點.故B正確.
的美好點.故B正確.
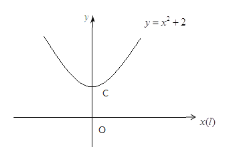
如下圖,拋物線的頂點C(0,2),所以![]() 上的點與
上的點與![]() 上的點之間最短距離是2,所以
上的點之間最短距離是2,所以![]() 上不存在
上不存在![]() 的美好點.
的美好點.
故答案為A,B.
(2)①如圖,當直線MN與⊙O相離時,因為M (![]() n, 0) , N (0, n)(
n, 0) , N (0, n)(![]() )所以直線MN的解析式為:
)所以直線MN的解析式為:![]() ,
,![]() ,
,
將直線NN平移到與⊙O相切,切點為E,與![]() 軸交于點C,連接OE,延長OE與MN交于點D,則
軸交于點C,連接OE,延長OE與MN交于點D,則![]() ,當E為MN的美好點時,此時⊙O 上存在一個MN的美好點,此時ED=
,當E為MN的美好點時,此時⊙O 上存在一個MN的美好點,此時ED=![]() ,所以當⊙O上恰好存在MN的兩個美好點,則
,所以當⊙O上恰好存在MN的兩個美好點,則![]() ,
,
又由![]() 所以
所以![]() ,所以
,所以![]() ,
,
所以![]() ,解得:
,解得:![]() .
.
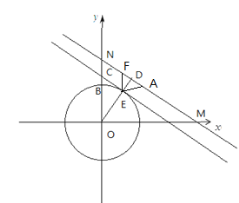
當直線MN與⊙O相交時,如下圖,同理當![]() 時,由對稱性知道⊙O上存在MN的三個美好點,然后會出現四個美好點,所以此時
時,由對稱性知道⊙O上存在MN的三個美好點,然后會出現四個美好點,所以此時![]() ,此時
,此時![]() ,所以
,所以![]() ,解得:
,解得:![]() .綜上
.綜上![]() 的取值范圍為:
的取值范圍為:![]() .
.
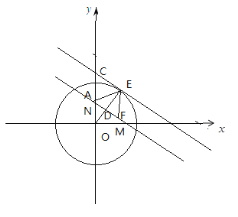
②如下圖,當n4,則M (![]() , 0) , N (0, 4),此時
, 0) , N (0, 4),此時![]() ,將直線NN平移到與⊙O相切,切點為E,與
,將直線NN平移到與⊙O相切,切點為E,與![]() 軸交于點C,連接OE,延長OE與MN交于點D,則
軸交于點C,連接OE,延長OE與MN交于點D,則![]() ,當E為MN的美好點時,此時⊙O 上存在一個MN的美好點,此時ED=
,當E為MN的美好點時,此時⊙O 上存在一個MN的美好點,此時ED=![]() ,若線段 MN 上存在⊙O 的“美好點”,則
,若線段 MN 上存在⊙O 的“美好點”,則![]() ,
,
所以![]() ,解得:
,解得:![]()


科目:初中數學 來源: 題型:
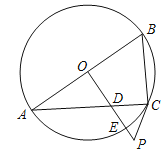
【題目】如圖,已知AB是⊙O的直徑,過O點作OP⊥AB,交弦AC于點D,交⊙O于點E,且使∠PCA=∠ABC.
(1)求證:PC是⊙O的切線;
(2)若∠P=60°,PC=2,求PE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1)所示,E為矩形ABCD的邊AD上一點,動點P,Q同時從點B出發,點P沿折線BE-ED-DC運動到點C時停止,點Q沿BC運動到點C時停止,它們運動的速度都是1cm/秒.設P、Q同時出發t秒時,△BPQ的面積為ycm2.已知y與t的函數關系圖象如圖(2)(曲線OM為拋物線的一部分),則下列結論:①AD=BE=5;②![]() ;③當0<t≤5時,
;③當0<t≤5時,![]() ;④當
;④當![]() 秒時,△ABE∽△QBP;其中正確的結論是( )
秒時,△ABE∽△QBP;其中正確的結論是( )
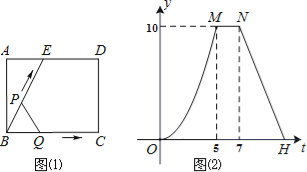
A. ①②③B. ②③C. ①③④D. ②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC邊上一點,且DA=DB,O是AB的中點,CE是△BCD的中線.
(1)如圖a,連接OC,請直接寫出∠OCE和∠OAC的數量關系: ;
(2)點M是射線EC上的一個動點,將射線OM繞點O逆時針旋轉得射線ON,使∠MON=∠ADB,ON與射線CA交于點N.
①如圖b,猜想并證明線段OM和線段ON之間的數量關系;
②若∠BAC=30°,BC=m,當∠AON=15°時,請直接寫出線段ME的長度(用含m的代數式表示).
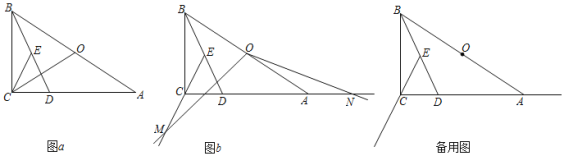
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個函數的解析式等于另兩個函數解析式的和,則這個函數稱為另兩個函數的“生成函數”。現有關于x的兩個二次函數y1、y2,且y1=a(x-m)2+4(m>0),y1、y2的“生成函數”為:y=x2+4x+14;當x=m時,y2=15;二次函數y2的圖象的頂點坐標為(2,k)。
(1)求m的值;
(2)求二次函數y1、y2的解析式。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為備戰奧運會,中國女排的姑娘們刻苦訓練,為國爭光,如圖,已知排球場的長度 OD 為 18 米,位于球場中線處球網的高度 AB 為 2.43 米,一隊員站在點 O 處發球,排球從點 O 的正上方 1.8 米的 C 點向正前方飛出,當排球運行至離點 O 的水平距離 OE 為 7 米時,到達最高點 G,建立如圖所示的平面直角坐標系.
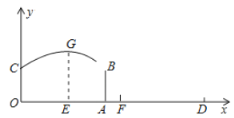
(1)當球上升的最大高度為 3.2 米時,求排球飛行的高度 y(單位:米)與水平距離 x(單位:米)的函數關系式.(不要求寫出自變量 x 的取值范圍)
(2)在(1)的條件下,對方距球網 0.5 米的點 F 處有一隊員,她起跳后的最大高度為 3.1米,問這次她是否可以攔網成功?請通過計算說明.(不考慮排球的大小)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是拋物線型拱橋,當拱頂離水面![]() 時,水面寬
時,水面寬![]() 為
為![]() .當水面上升
.當水面上升![]() 時達到警戒水位,此時拱橋內的水面寬度是多少
時達到警戒水位,此時拱橋內的水面寬度是多少![]() ?
?
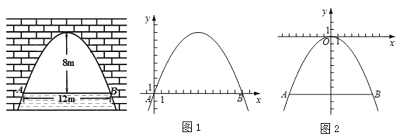
下面給出了解決這個問題的兩種方法,請補充完整:
方法一:如圖1.以點![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,建立平面直角坐標系
軸,建立平面直角坐標系![]() ,此時點
,此時點![]() 的坐標為_______,拋物線的項點坐標為_______,可求這條拋物線所表示的二次函數解析式為_______.當
的坐標為_______,拋物線的項點坐標為_______,可求這條拋物線所表示的二次函數解析式為_______.當![]() 時,求出此時自變量
時,求出此時自變量![]() 的取值,即可解決這個問題.
的取值,即可解決這個問題.
方法二:如圖2,以拋物線頂點為原點,對稱軸為![]() 軸.建立平面直角坐標系
軸.建立平面直角坐標系![]() ,這時這條拋物線所表示的二次函數的解析式為_______,當水面達到警戒水位,即
,這時這條拋物線所表示的二次函數的解析式為_______,當水面達到警戒水位,即![]() _______時,求出此時自變量
_______時,求出此時自變量![]() 的取值為_______,從而得水面寬為
的取值為_______,從而得水面寬為![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
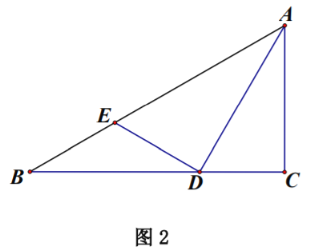
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 、 點
、 點![]() 分別在線段
分別在線段![]() 和線段
和線段![]() 上,
上, ![]() 平分
平分![]() .
.
![]() 如圖1,求證:
如圖1,求證:![]() .
.
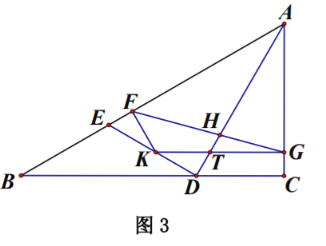
![]() 如圖2,若
如圖2,若![]() .求證:
.求證:![]() .
.
![]() 在
在![]() 問的條件下,如圖3, 在線段
問的條件下,如圖3, 在線段![]() 上取一點
上取一點![]() ,使
,使![]() .過點
.過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,作
,作![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,交
,交![]() 于點
于點![]() ,若
,若![]() ,求
,求![]() 的長.
的長.
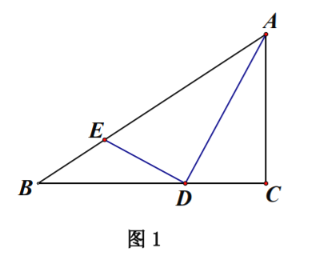
查看答案和解析>>
科目:初中數學 來源: 題型:
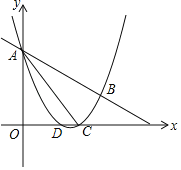
【題目】如圖,拋物線![]() 與直線
與直線![]() 交于A,B兩點,交x軸與D,C兩點,連接AC,已知A(0,3),C(3,0).(1)拋物線的解析式__;(2)設E為線段AC上一點(不含端點),連接DE,一動點M從點D出發,沿線段DE以每秒一個單位速度運動到E點,再沿線段EA以每秒
交于A,B兩點,交x軸與D,C兩點,連接AC,已知A(0,3),C(3,0).(1)拋物線的解析式__;(2)設E為線段AC上一點(不含端點),連接DE,一動點M從點D出發,沿線段DE以每秒一個單位速度運動到E點,再沿線段EA以每秒![]() 個單位的速度運動到A后停止.若使點M在整個運動中用時最少,則點E的坐標__.
個單位的速度運動到A后停止.若使點M在整個運動中用時最少,則點E的坐標__.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com