
分析 (1)根據題意可以求得y與x的函數關系式,由供貨商規定這種空氣凈化器售價不能低于600元/臺,代理銷售商每月要完成不低于60臺的銷售任務可以求得x的取值范圍;
(2)根據題意可以得到w關于x的關系式,然后化為頂點式,從而可以求得w的最大值和此時x的值.
解答 解:(1)由題意可得,
y=50+(1000-x)÷20×5=300-$\frac{x}{4}$,
∵貨商規定這種空氣凈化器售價不能低于600元/臺,代理銷售商每月要完成不低于60臺的銷售任務,
∴$\left\{\begin{array}{l}{x≥600}\\{300-\frac{x}{4}≥60}\end{array}\right.$,
解得,600≤x≤960,
即月銷售量y(臺)與售價x(元/臺)之間的函數關系式是y=300-$\frac{x}{4}$(600≤x≤960);
(2)由題意可得,
w=(x-500)(300-$\frac{x}{4}$)=$-\frac{1}{4}(x-850)^{2}+30625$,
∴當x=850時,w取得最大值,此時w=30625,
即當售價x定為850元/臺時,商場每月銷售這種空氣凈化器所獲得的利潤w(元)最大,最大利潤是30625元.
點評 本題考查二次函數的應用,解題的關鍵是明確題意,找出所求問題需要的條件.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:解答題
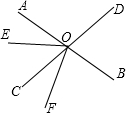 如圖,直線AB、CD相交于點O.已知∠BOD=75°,OE把∠AOC分成兩個角,且∠AOE:∠EOC=2:3.
如圖,直線AB、CD相交于點O.已知∠BOD=75°,OE把∠AOC分成兩個角,且∠AOE:∠EOC=2:3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com