
(本題10分)在Rt△ABC中,∠CAB=90°,AB=AC.
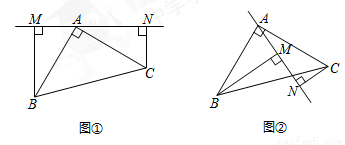
(1)如圖①,過點A在△ABC外作直線MN,BM⊥MN于M,CN⊥MN于N.
①判斷線段MN、BM、CN之間有何數量關系,并證明;
②若AM=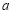 ,BM=
,BM= ,AB=
,AB= ,試利用圖①驗證勾股定理
,試利用圖①驗證勾股定理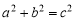 ;
;
(2)如圖②,過點A在△ABC內作直線MN,BM⊥MN于M,CN⊥MN于N,判斷線段MN、BM、CN之間有何數量關系?(直接寫出答案)
(1)①MN=BM+CN,理由見試題解析;②證明見試題解析;(2)MN=BM﹣CN.
【解析】
試題分析:(1)①利用已知得出∠MAB=∠ACN,進而得出△MAB≌△NCA,進而得出BM=AN,AM=CN,即可得出線段MN、BM、CN之間的數量關系;
②利用S梯形MBCN=S△MAB+S△ABC+S△NCA,S梯形MBCN=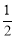 (BM+CN)×MN=
(BM+CN)×MN=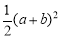 ,進而得出答案;
,進而得出答案;
(2)利用已知得出∠MAB=∠ACN,進而得出△MAB≌△NCA,進而得出BM=AN,AM=CN,即可得出線段MN、BM、CN之間的數量關系.
試題解析:(1)①MN=BM+CN;
理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,∴∠MAB=∠ACN,
在△MAB和△NCA中,∵∠BMA=∠ANC,∠MAB=∠NCA,AB=AC,∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,∴MN=AM+AN=BM+CN;
②由①知△MAB≌△NCA,∴CN=AM=a,AN=BM=b,AC=BC=c,∴MN=a+b,
∵S梯形MBCN=S△MAB+S△ABC+S△NCA=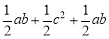 ,S梯形MBCN=
,S梯形MBCN=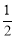 (BM+CN)×MN=
(BM+CN)×MN=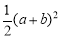 ,
,
∴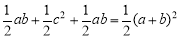 ,∴
,∴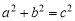 ;
;
(2)MN=BM﹣CN;
理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,∴∠MAB=∠ACN,
在△MAB和△NCA中,∵∠BMA=∠ANC,∠MAB=∠NCA,AB=AC,∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,∴MN=AN﹣AM=BM﹣CN.
考點:全等三角形的判定與性質.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:2014-2015學年江蘇省興華顧莊等三校九年級上學期期中考試數學試卷(解析版) 題型:解答題
當自變量x =4時,二次函數有最小值 3,且它的圖像與x軸的一個交點的橫坐標為1.求這個二次函數的表達式.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省興化顧莊等三校八年級上學期期中聯考數學試卷(解析版) 題型:選擇題
在平面直角坐標系中,點A(-2, 3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省興化顧莊等三校七年級上學期期中聯考數學試卷(解析版) 題型:選擇題
將數據36 000 000用科學記數法表示是
A.3.6×107 B.0.36×108 C.36×107 D.3.6×106
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省丹陽市八年級上學期期中考試數學試卷(解析版) 題型:解答題
(本題7分)如圖,在長度為1個單位長度的正方形網格中,點A、B、C在小正方形的頂點上.

(1)在圖中畫出與△ABC關于直線l成軸對稱的△A′B′C′;則點B′、 C′的坐標分別為( 、 ) ( 、 )
(2)在直線l上找一點P(在答題紙上圖中標出),使PB+PC的長最短,這個最短長度的平方值是 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省東臺市九年級上學期期中考試數學試卷(解析版) 題型:解答題
(10分)某校學生會向全校1900名學生發起了愛心捐款活動,為了解捐款情況,學生會隨機調查了部分學生的捐款金額,并用得到的數據繪制了如下統計圖①和圖②,請根據相關信息,解答下列問題:
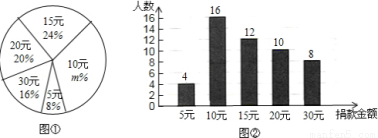
(1)本次接受隨機抽樣調查的學生人數為________ ,圖①中m的值是________;
(2)求本次調查獲取的樣本數據的平均數、眾數和中位數;
(3)根據樣本數據,估計該校本次活動捐款金額為10元的學生人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com