
 如圖,在Rt△ABC中,∠ABC=90°∠A=30°,AC=10,把Rt△ABC繞點B順時針旋轉到△A′BC′的位置,點C′在AC上,A′C′與AB相交于點D,則C′D的長為$\frac{5}{2}$.
如圖,在Rt△ABC中,∠ABC=90°∠A=30°,AC=10,把Rt△ABC繞點B順時針旋轉到△A′BC′的位置,點C′在AC上,A′C′與AB相交于點D,則C′D的長為$\frac{5}{2}$. 分析 根據在Rt△ABC中,∠ABC=90°∠A=30°,AC=10,可以求得BC的長,∠C的度數,又因為Rt△ABC繞點B順時針旋轉到△A′BC′的位置,點C′在AC上,A′C′與AB相交于點D,可以求得旋轉前后的對應邊和對應角是相等的,從而可以得到C′D的長,本題得以解決.
解答 解:∵在Rt△ABC中,∠ABC=90°∠A=30°,AC=10,
∴$BC=\frac{1}{2}AC=5$,∠C=60°,
∵Rt△ABC繞點B順時針旋轉到△A′BC′的位置,點C′在AC上,A′C′與AB相交于點D,∠C=60°,
∴BC=BC′,∠BC′D=∠C=60°,
∴△CBC′是等邊三角形,
∴CC′=BC=5,∠CC′B=60°,
∴∠AC′D=60°,
∵∠A=30°,AC=10,CC′=5,
∴∠ADC′=90°,AC′=5,
∴C′D=$\frac{1}{2}AC′=\frac{5}{2}$.
故答案為:$\frac{5}{2}$.
點評 本題考查旋轉的性質,解題的關鍵是明確在直角三角形中30°角所對的直角邊等于斜邊的一半和明確旋轉前后對應邊和對應角是相等的.


科目:初中數學 來源: 題型:解答題
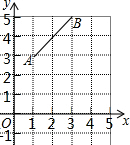 如圖,在平面直角坐標系中,把線段AB先向右平移2個單位,再向下平移3個單位,得到線段CD,請畫出線段CD并分別寫出點A、B、C、D的坐標.
如圖,在平面直角坐標系中,把線段AB先向右平移2個單位,再向下平移3個單位,得到線段CD,請畫出線段CD并分別寫出點A、B、C、D的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖是某個正方體的表面展開圖,各個面上分別標有1-6的不同數字,若將其折疊成正方體,則相交于同一個頂點的三個面上的數字之和最大的是13.
如圖是某個正方體的表面展開圖,各個面上分別標有1-6的不同數字,若將其折疊成正方體,則相交于同一個頂點的三個面上的數字之和最大的是13.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com