九九视频在线,亚洲成人动漫在线观看,人人干视频

古希臘著名的畢達哥拉斯學派把1，3，6，10 …這樣的數稱為“三角形數”，而把1，4，9，16 …這樣的數稱為“正方數”．從圖中可以發現，任何一個大于1的“正方形數”都可以看作兩個相鄰“三角形數”之和．下列等式中，符合這一規律的是（）

A．20=6+14 B．25=9+16 C．36=16+20 D．49=21+28

D．

【解析】

試題分析：本題考查探究、歸納的數學思想方法．題中明確指出：任何一個大于1的“正方形數”都可以看作兩個相鄰“三角形數”之和．由于“正方形數”為兩個“三角形數”之和，正方形數可以用代數式表示為：（n+1）2，兩個三角形數分別表示為n（n+1）和（n+1）（n+2），所以由正方形數可以推得n的值，然后求得三角形數的值．

【解析】
根據規律：正方形數可以用代數式表示為：（n+1）2，

兩個三角形數分別表示為n（n+1）和（n+1）（n+2），

只有D、49=21+28符合，

故選D．

考點：找規律.

練習冊系列答案

優翼專項小學升學總復習系統強化訓練系列答案

小學升初中奪冠密卷系列答案

小學升初中核心試卷系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源：2014-2015學年重慶市等五校九年級上學期期中聯考數學試卷（解析版） 題型：解答題

已知等腰Rt△ABC中，∠ACB=90°，AC=BC，點G在BC上，連接AG，過C作CF⊥AG，垂足為點E，過點B作BF⊥CF于點F，點D是AB的中點，連接DE、DF

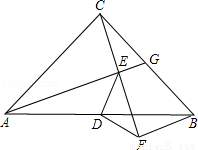
（1）若∠CAG=30°，EG=1，求BG的長；

（2）求證：∠AED=∠DFE．

查看答案和解析>>

科目：初中數學 來源：2014-2015學年重慶市校七年級12月月考數學試卷（解析版） 題型：填空題

2014年12月8日“全國目標教學展示”在71中舉行。來自全國的選手共展示了47節課，參加聽課的師生共有2748人次，請將2748用用科學計數法表示為________

查看答案和解析>>

科目：初中數學 來源：2014-2015學年重慶市校八年級12月月考數學試卷（解析版） 題型：解答題

（1）如圖1，已知：在△ABC中，∠BAC＝90°，AB=AC，直線m經過點A，BD⊥直線m，CE⊥直線m，垂足分別為點D、E．證明：DE=BD+CE．

（2）如圖2，將（1）中的條件改為：在△ABC中，AB=AC，D、A、E三點都在直線m上，并且有∠BDA=∠AEC=∠BAC=，其中為任意銳角或鈍角．請問結論“DE=BD+CE”是否成立?如成立，請你給出證明；若不成立，請說明理由．

（3）如圖3，D、E是D、A、E三點所在直線m上的兩動點（D、A、E三點互不重合），點F為∠BAC平分線上的一點，且△ABF和△ACF均為等邊三角形，連接BD、CE，若∠BDA=∠AEC=∠BAC，試判斷△DEF的形狀．

查看答案和解析>>

科目：初中數學 來源：2014-2015學年重慶市校八年級12月月考數學試卷（解析版） 題型：填空題

如圖，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的頂點P是BC的中點，兩邊PE、PF分別交AB、AC于點E、F，給出以下五個結論：①AE=CF；②∠APE=∠CPF；③△EPF是等腰直角三角形；④EF=AP；⑤．當∠EPF在△ABC內繞頂點P旋轉時（點E不與點A、B重合），上述結論中始終正確的序號有．