
 在直角坐標系xOy中(如圖),拋物線y=ax2-4ax+4a+3(a<0)的頂點為D,它的對稱軸與x軸交點為M.
在直角坐標系xOy中(如圖),拋物線y=ax2-4ax+4a+3(a<0)的頂點為D,它的對稱軸與x軸交點為M.分析 (1)由y=ax2-4ax+4a+3=a(x-2)2+3,可得頂點D(2,3),M(2,0).
(2)作PN⊥DM于N.由△PDN∽△MAO,得$\frac{PN}{OM}$=$\frac{DN}{OA}$=$\frac{PD}{AM}$=$\frac{1}{2}$,因為OM=2,OA=-4a-3,PN=1,所以P(1,a+3),DN=-a,根據OA=2DN,可得方程-4a-3=-2a,由此即可解決問題.
解答 解:(1)∵y=ax2-4ax+4a+3=a(x-2)2+3,
∴頂點D(2,3),M(2,0).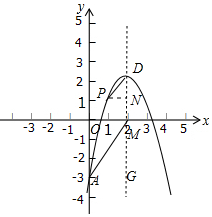
(2)作PN⊥DM于N.
∵AM∥DP,
∴∠PDN=∠AMG,
∵DG∥OA,
∴∠OAM=∠AMG=∠PDN,
∵∠PND=∠AOM=90°,
∴△PDN∽△MAO,
∴$\frac{PN}{OM}$=$\frac{DN}{OA}$=$\frac{PD}{AM}$=$\frac{1}{2}$,
∵OM=2,OA=-4a-3,PN=1,
∴P(1,a+3),
∴DN=-a,
∵OA=2DN,
∴-4a-3=-2a,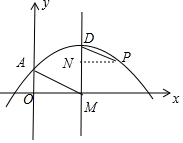
∴a=-$\frac{3}{2}$.
當點A在y的正半軸上時,如圖,
∴△PDN∽△MAO,
∴$\frac{PN}{OM}$=$\frac{DN}{OA}$=$\frac{PD}{AM}$=$\frac{1}{2}$,
∵OM=2,OA=4a+3,PN=1,
∴P(3,a+3),
∴DN=-a,
∵OA=2DN,
∴4a+3=-2a,
∴a=-$\frac{1}{2}$,
綜上所述,滿足條件的a的值為-$\frac{1}{2}$或-$\frac{3}{2}$.
點評 本題考查拋物線與x軸的交點、相似三角形的判定和性質等知識,解題的關鍵是靈活運用所學知識解決問題,學會利用相似三角形的性質解決問題,用方程的思想思考問題,屬于中考常考題型.


 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:解答題
| (1)(+9)-(-9); | (2)-6+(+6); | (3)$\frac{1}{3}$+(-$\frac{1}{2}$); | (4)0.5-(+$\frac{1}{5}$); |
| (5)0.8+(-1.2); | (6)-1×(-2)×(-3); | (7)(-$\frac{1}{4}$)×(-$\frac{2}{5}$)×20; | (8)(-1)2×(-22); |
| (9)-23×(-3)2×(-1)3; | (10)(-12)÷(-$\frac{4}{7}$)×0. |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
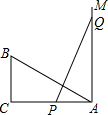 如圖所示,有一個直角△ABC,∠C=90°,AC=10,BC=5,一條線段PQ=AB,P、Q兩點分別在AC和過點A垂直于AC的射線AM上運動,當AP=5時,才能使△ABC≌△QPA.
如圖所示,有一個直角△ABC,∠C=90°,AC=10,BC=5,一條線段PQ=AB,P、Q兩點分別在AC和過點A垂直于AC的射線AM上運動,當AP=5時,才能使△ABC≌△QPA.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com