
| 解法一:過D作DG∥AB交BC于G,∵AD∥BC,AB∥DG,
∴四邊形ABGD是平行四邊形,∴AB=DG. ∵EF∥AB,∴EF∥DG.∵DE=CE,∴GF=CF. ∴EF是△CDG的中位線.∴EF= ∴DG=2EF=6,即AB=6. 解法二:過點E作EH∥BC交AB于H(如圖). ∵EH∥BC,EF∥AB,∴四邊形HBFE是平行四邊形. ∴BH=EF=3.∵DE=CE, ∴AH=BH.∴AB=2BH=6. 說明:涉及中點的問題,經常需要轉化為中位線來解決,其中作輔助平行線是解題的關鍵,通過作平行線可以構造中位線,從而使問題得以解決.
|
| 導析:題目中涉及E是DC的中點,但無法直接應用,因此需構造與之相應的條件,由已知EF的長,求AB的長,這兩個量也無直接關系,因此想到平移AB,通過中位線使已知與未知得以溝通.
|


科目:初中數學 來源: 題型:
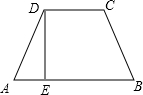 如圖,在梯形ABCD中,BC=AD,DC∥AB,DE⊥AB于E,下列結論正確的是( )
如圖,在梯形ABCD中,BC=AD,DC∥AB,DE⊥AB于E,下列結論正確的是( )| A、AE=AB-DC | ||
B、AE=
| ||
| C、AD+BC=AB+DC | ||
D、AB-DC=
|
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在梯形ABCD中,AB∥DC.
如圖,在梯形ABCD中,AB∥DC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com