
【題目】如圖1,在![]() 中,
中,![]() 為銳角.點
為銳角.點![]() 為射線
為射線![]() 上一動點,連接
上一動點,連接![]() ,以
,以![]() 為一邊且在
為一邊且在![]() 的右側作正方形
的右側作正方形![]() .
.
解答下列問題:
![]() 如果
如果![]() ,
,![]() .
.
①當點![]() 在線段
在線段![]() 上時(與點
上時(與點![]() 不重合),如圖2,線段
不重合),如圖2,線段![]() 、
、![]() 之間的位置關系為________,數量關系為________.
之間的位置關系為________,數量關系為________.
②當點![]() 在線段
在線段![]() 的延長線上時,如圖3,①中的結論是否仍然成立,為什么?
的延長線上時,如圖3,①中的結論是否仍然成立,為什么?
![]() 如果
如果![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上運動.試探究:當
上運動.試探究:當![]() 滿足一個什么條件時,
滿足一個什么條件時,![]() (點
(點![]() 、
、![]() 重合除外)?畫出相應圖形,并說明理由.(畫圖不寫作法)
重合除外)?畫出相應圖形,并說明理由.(畫圖不寫作法)

【答案】(1)垂直,相等; ![]() 當
當![]() 時,
時,![]() ,理由見解析.
,理由見解析.
【解析】
(1)①根據正方形的性質得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根據全等三角形的性質即可得到結論;②由正方形ADEF的性質可推出△DAB≌△FAC,根據全等三角形的性質得到CF=BD,∠ACF=∠ABD,根據余角的性質即可得到結論;
(2)過點A作AG⊥AC交CB或CB的延長線于點G,于是得到∠GAC=90°,可推出∠ACB=∠AGC,證得AC=AG,根據(1)的結論于是得到結果.
(1)①正方形ADEF中,AD=AF.
∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF.在△DAB與△FAC中,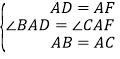 ,∴△DAB≌△FAC,∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.
,∴△DAB≌△FAC,∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.
故答案為:垂直、相等;
②成立,理由如下:
∵∠FAD=∠BAC=90°
∴∠BAD=∠CAF
在△BAD與△CAF中,∵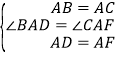 ,∴△BAD≌△CAF,∴CF=BD,∠ACF=∠ACB=45°,∴∠BCF=90°,∴CF⊥BD;
,∴△BAD≌△CAF,∴CF=BD,∠ACF=∠ACB=45°,∴∠BCF=90°,∴CF⊥BD;
(2)當∠ACB=45°時,CF⊥BD(如圖).
理由:過點A作AG⊥AC交CB的延長線于點G,則∠GAC=90°.
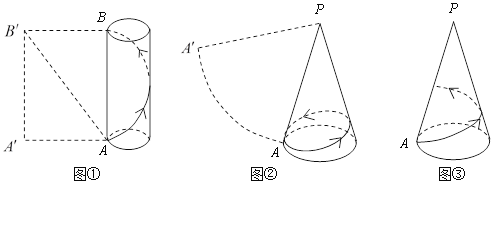
∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG.在△GAD與△CAF中,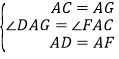 ,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知:在△ABC和△AEF中,點E在BC邊上,AE=AB,AC=AF,∠CAF=∠BAE,EF與AC交于點G.

(1)求證:EF=BC;
(2)若∠ABC=65°.∠ACB=28°,求∠FGC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種型號油電混合動力汽車,從A地到B地燃油行駛純燃油費用76元,從A地到B地用電行駛純電費用26元,已知每行駛1千米,純燃油費用比純用電費用多0.5元.
(1)求每行駛1千米純用電的費用;
(2)若要使從A地到B地油電混合行駛所需的油、電費用合計不超過39元,則至少用電行駛多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△OAC中,以O為圓心,OA為半徑作⊙O,作OB⊥OC交⊙O于B,垂足為O,連接AB交OC于點D,∠CAD=∠CDA.
(1)判斷AC與⊙O的位置關系,并證明你的結論;
(2)若OA=5,OD=1,求線段AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉角
順時針旋轉角![]() 得
得![]() ,
,![]() 交
交![]() 于點
于點![]() ,
,![]() 分別交
分別交![]() 、
、![]() 于
于![]() 、
、![]() 兩點.
兩點.
![]() 如圖
如圖![]() ,觀察并猜想:圖中在不連接其它線段的情況下,共有多少對全等三角形(不包含
,觀察并猜想:圖中在不連接其它線段的情況下,共有多少對全等三角形(不包含![]() )?將它們全部寫出來,并且選一組全等三角形進行證明;
)?將它們全部寫出來,并且選一組全等三角形進行證明;
![]() 如圖
如圖![]() ,當
,當![]() 時,求
時,求![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠修建了甲、乙兩個水池,最大蓄水量都是1200立方米,如果甲池有水480立方米,乙池蓄滿水,甲池每小時進水80立方米,乙池每小時放水100立方米.
(1)分別寫出甲、乙兩池的水量![]() 與時間
與時間![]() 的函數解析式;
的函數解析式;
(2)甲、乙兩池同時進水、放水,經過幾小時兩個水池內的水一樣多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題探究:
(1)如圖①所示是一個半徑為![]() ,高為4的圓柱體和它的側面展開圖,AB是圓柱的一條母線,一只螞蟻從A點出發沿圓柱的側面爬行一周到達B點,求螞蟻爬行的最短路程.(探究思路:將圓柱的側面沿母線AB剪開,它的側面展開圖如圖①中的矩形
,高為4的圓柱體和它的側面展開圖,AB是圓柱的一條母線,一只螞蟻從A點出發沿圓柱的側面爬行一周到達B點,求螞蟻爬行的最短路程.(探究思路:將圓柱的側面沿母線AB剪開,它的側面展開圖如圖①中的矩形![]() 則螞蟻爬行的最短路程即為線段
則螞蟻爬行的最短路程即為線段![]() 的長)
的長)
(2)如圖②所示是一個底面半徑為![]() ,母線長為4的圓錐和它的側面展開圖,PA是它的一條母線,一只螞蟻從A點出發沿圓錐的側面爬行一周后回到A點,求螞蟻爬行的最短路程.
,母線長為4的圓錐和它的側面展開圖,PA是它的一條母線,一只螞蟻從A點出發沿圓錐的側面爬行一周后回到A點,求螞蟻爬行的最短路程.
(3)如圖③所示,在②的條件下,一只螞蟻從A點出發沿圓錐的側面爬行一周到達母線PA上的一點,求螞蟻爬行的最短路程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 圖象
圖象![]() 軸上方的部分沿
軸上方的部分沿![]() 軸翻折到
軸翻折到![]() 軸下方,圖象的其余部分保持不變,翻折后的圖象與原圖象
軸下方,圖象的其余部分保持不變,翻折后的圖象與原圖象![]() 軸下方的部分組成一個“
軸下方的部分組成一個“![]() ”形狀的新圖象,若直線
”形狀的新圖象,若直線![]() 與該新圖象有兩個公共點,則
與該新圖象有兩個公共點,則![]() 的取值范圍為_____.
的取值范圍為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com