
分析 (1)仿照例題,式子乘1后結果不變,所以式子乘(2-1),反復運用平方差公式,得出結果;
(2)仿照例題,式子乘1后結果不變,所以式子乘$\frac{1}{2}$(3-1)后,運用平方差公式,計算出結果.
解答 解:(2+1)(22+1)(24+1)(28+1)…(264+1)
=(2-1)(2+1)(22+1)(24+1)(28+1)…(264+1)
=(22-1)(22+1)(24+1)(28+1)…(264+1)
=2128-1;
(2)(3+1)(32+1)(34+1)(38+1)…(3n+1)-$\frac{{9}^{n}}{2}$
=$\frac{1}{2}(3-1)$(3+1)(32+1)(34+1)(38+1)…(3n+1)-$\frac{{9}^{n}}{2}$
=$\frac{1}{2}$(32n-1)-$\frac{{9}^{n}}{2}$
=$\frac{{9}^{n}}{2}-\frac{1}{2}-\frac{{9}^{n}}{2}$
=-$\frac{1}{2}$.
點評 本題主要考查了平方差公式.解決本題的關鍵是式子乘以(2-1)、$\frac{1}{2}$(3-1)后,運用平方差公式.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
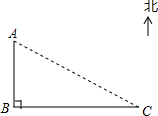 如圖,在海上觀察所A處.我邊防海警發現正南方向60海里的B處有一可疑船只正以每小時20海里的速度向正東方向C處駛去,我邊防海警即刻從A處派快艇去攔截.若快艇的速度是每小時$\frac{100}{3}$海里.問快艇最快幾小時攔截住可疑船只?
如圖,在海上觀察所A處.我邊防海警發現正南方向60海里的B處有一可疑船只正以每小時20海里的速度向正東方向C處駛去,我邊防海警即刻從A處派快艇去攔截.若快艇的速度是每小時$\frac{100}{3}$海里.問快艇最快幾小時攔截住可疑船只?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com