Question

如圖，利用一面墻（墻的長度不超過45m），用80m長的籬笆圍一個矩形場地.

（1）怎樣圍才能使矩形場地的面積為750m²？

（2）能否使所圍矩形場地的面積為810 m²，為什么？

 

Answer 1

【答案】

（1）當所圍矩形的長為30m、寬為25m時，能使矩形的面積為750m²；（2）不能．

【解析】

試題分析：（1）設所圍矩形ABCD的長AB為x米，則寬AD為 米，根據矩形面積的計算方法列出方程求解；（2）假使矩形面積為810米，則方程無實數根，所以不能圍成矩形場地．

試題解析：（1）設所圍矩形ABCD的長AB為x米，則寬AD為米．

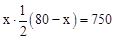依題意，得，即.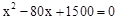

解此方程，得x₁=30，x₂=50.

∵墻的長度不超過45m，∴x₂=50不合題意，應舍去．

當x=30時，.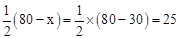

答：當所圍矩形的長為30m、寬為25m時，能使矩形的面積為750m²．

（2）不能．理由如下：

由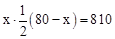得．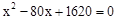

∵，

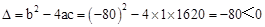∴方程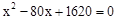沒有實數根．

∴不能使所圍矩形場地的面積為810m²．

考點：1.一元二次方程的應用（幾何問題）；2. 矩形的性質；3.一元二次方程根的判別式.