
如圖,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O為原點,OC、OA所在直線為軸建立坐標系.拋物線頂點為A,且經過點C.點P在線段AO上由A向點O運動,點O在線段OC上由C向點O運動,QD⊥OC交BC于點D,OD所在直線與拋物線在第一象限交于點E.
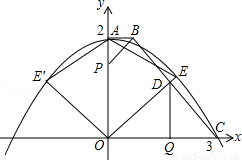
(1)求拋物線的解析式;
(2)點E′是E關于y軸的對稱點,點Q運動到何處時,四邊形OEAE′是菱形?
(3)點P、Q分別以每秒2個單位和3個單位的速度同時出發,運動的時間為t秒,當t為何值時,PB∥OD?
解:(1)∵A(0,2)為拋物線的頂點,∴設y=ax2+2。
∵點C(3,0),在拋物線上,∴9a+2=0,解得: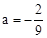 。
。
∴拋物線的解析式為;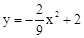 。
。
(2)若要四邊形OEAE′是菱形,則只要AO與EE′互相垂直平分,
∴EE′經過AO的中點,∴點E縱坐標為1,代入拋物線解析式得: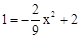 ,
,
解得: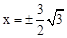 。
。
∵點E在第一象限,∴點E為(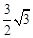 ,1)。
,1)。
設直線BC的解析式為y=kx+b,
把B(1,2),C(3,0),代入得: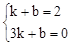 ,解得
,解得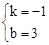 。
。
∴BC的解析式為: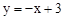 。
。
設直線EO的解析式為y=ax,將E點代入,可得出EO的解析式為: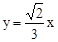 。
。
由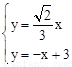 ,得:
,得: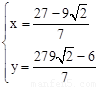 ,
,
∴直線EO和直線BC的交點坐標為:( ,
,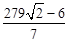 )。
)。
∴Q點坐標為:( ,0)。
,0)。
∴當Q點坐標為( ,0)時,四邊形OEAE′是菱形。
,0)時,四邊形OEAE′是菱形。
(3)設t為m秒時,PB∥DO,又QD∥y軸,則有∠APB=∠AOE=∠ODQ,
又∵∠BAP=∠DQO,則有△APB∽△QDO。
∴ 。
。
由題意得:AB=1,AP=2m,QO=3﹣3m,
又∵點D在直線y=﹣x+3上,∴DQ=3m。
∴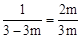 ,解得:
,解得: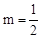 。
。
經檢驗: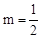 是原分式方程的解。
是原分式方程的解。
∴當t=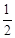 秒時,PB∥OD。
秒時,PB∥OD。
【解析】(1)根據頂點式將A,C代入解析式求出a的值,進而得出二次函數解析式。
(2)利用菱形的判定得出AO與EE′互相垂直平分,利用E點縱坐標得出x的值,進而得出BC,EO直線解析式,再利用兩直線交點坐標求法得出Q點坐標,即可得出答案。
(3)首先得出△APB∽△QDO,進而得出 ,求出m的值,進而得出答案。
,求出m的值,進而得出答案。


科目:初中數學 來源: 題型:
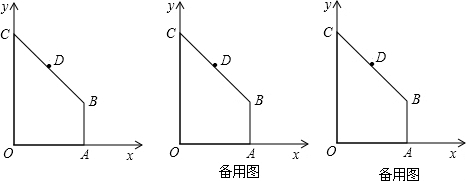
 如圖,在直角梯形ABCD中,AD∥BC,∠ABC=90°,中位線EF分別交BD,AC于點G,H,∠ACB=30°,則下列結論中正確的有
如圖,在直角梯形ABCD中,AD∥BC,∠ABC=90°,中位線EF分別交BD,AC于點G,H,∠ACB=30°,則下列結論中正確的有查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
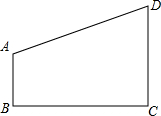 如圖,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=4,BC=5
如圖,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=4,BC=5| 6 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•郴州)如圖,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O為原點,OC、OA所在直線為軸建立坐標系.拋物線頂點為A,且經過點C.點P在線段AO上由A向點O運動,點Q在線段OC上由C向點O運動,QD⊥OC交BC于點D,OD所在直線與拋物線在第一象限交于點E.
(2013•郴州)如圖,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O為原點,OC、OA所在直線為軸建立坐標系.拋物線頂點為A,且經過點C.點P在線段AO上由A向點O運動,點Q在線段OC上由C向點O運動,QD⊥OC交BC于點D,OD所在直線與拋物線在第一象限交于點E.查看答案和解析>>
科目:初中數學 來源:第34章《二次函數》中考題集(51):34.4 二次函數的應用(解析版) 題型:解答題
 ,CD=9.
,CD=9.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com