
【題目】閱讀材料,回答下列問題:
阿爾花拉子米(約780~約850),著名阿拉伯數學家、天文學家、地理學家,是代數與算術的整理者,被譽為“代數之父”.他利用正方形圖形巧妙解出了一元二次方程x2+2x﹣35=0的一個解.
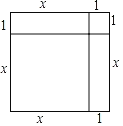
將邊長為x的正方形和邊長為1的正方形,外加兩個長方形,長為x,寬為1,拼合在一起面積就是x2+2×1+1×1,即x2+2x+1,而由原方程x2+2x﹣35=0變形得x2+2x+1=35+1,即右邊邊長為x+1的正方形面積為36.所以(x+1)2=36,則x=5.
(1)上述求解過程中所用的方法與下列哪種方法是一致的 .
A.直接開平方法 B.公式法
C.配方法 D.因式分解法
(2)所用的數學思想方法是 .
A.分類討論思想 B.數形結合思想 C.轉化思想
(3)運用上述方法構造出符合方程x2+4x﹣5=0的一個正根的正方形.
 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:初中數學 來源: 題型:
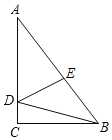
【題目】在Rt△ABC中,∠ACB=90°,AC=8,BC=6,點D、E分別在AC、AB上,且△ADE是直角三角形,△BDE是等腰三角形,則BE=_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
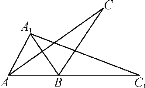
【題目】如圖,將一個鈍角△ABC(其中∠ABC=120°)繞點B順時針旋轉得△A1BC1,使得C點落在AB的延長線上的點C1處,連接AA1.
(1)寫出旋轉角的度數;
(2)求證:∠A1AC=∠C1.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,點M在BC邊上,且BM=![]() BC,AM與BD相交于點N,那么S△BMN:S平行四邊形ABCD為( )
BC,AM與BD相交于點N,那么S△BMN:S平行四邊形ABCD為( )

A.1:3B.1:9C.1:12D.1:24
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,動點P以
,動點P以![]() 的速度從A點出發,沿
的速度從A點出發,沿![]() 向C點移動,同時動點Q以
向C點移動,同時動點Q以![]() 的速度從點C出發,沿
的速度從點C出發,沿![]() 向點B移動,設P、Q兩點移動的時間為t秒
向點B移動,設P、Q兩點移動的時間為t秒![]() .
.
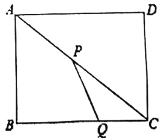
(1)t為多少時,以P、Q、C為頂點的三角形與![]() 相似?
相似?
(2)在P、Q兩點移動過程中,四邊形![]() 與
與![]() 的面積能否相等?若能,求出此時t的值;若不能,請說明理由.
的面積能否相等?若能,求出此時t的值;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD的外接圓為⊙O,AD是⊙O的直徑,過點B作⊙O的切線,交DA的延長線于點E,連接BD,且∠E=∠DBC.
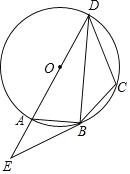
(1)求證:DB平分∠ADC;
(2)若EB=10,CD=9,tan∠ABE=![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
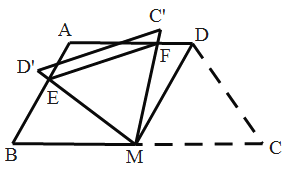
【題目】如圖,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,將
的中點,將![]() 繞點
繞點![]() 旋轉,當
旋轉,當![]() (即
(即![]() )與
)與![]() 交于一點
交于一點![]() ,
,![]() (
(![]() )同時與
)同時與![]() 交于一點
交于一點![]() 時,點
時,點![]() ,
,![]() 和點
和點![]() 構成
構成![]() ,在此過程中,
,在此過程中,![]() 周長的最小值是__________.
周長的最小值是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于的一元二次方程x2+2x+k+1=0的實數解是x1和x2.
(1)求k的取值范圍;
(2)如果x1+x2﹣x1x2<﹣1且k為整數,求k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com