
【題目】如圖,在3×3的正方形網格中標出了∠1和∠2.則∠1+∠2= .
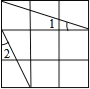
【答案】45°.
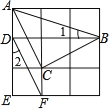
【解析】試題分析:根據圖形,先將角進行轉化,再根據勾股定理的逆定理,求得∠ACB=90°,由等腰三角形的性質,推得∠1+∠2=45°.
解:連接AC,BC.
根據勾股定理,AC=BC=![]() ,AB=
,AB=![]() .
.
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2,
)2,
∴∠ACB=90°,∠CAB=45°.
∵AD∥CF,AD=CF,
∴四邊形ADFC是平行四邊形,
∴AC∥DF,
∴∠2=∠DAC(兩直線平行,同位角相等),
在Rt△ABD中,
∠1+∠DAB=90°(直角三角形中的兩個銳角互余);
又∵∠DAB=∠DAC+∠CAB,
∴∠1+∠CAB+∠DAC=90°,
∴∠1+∠DAC=45°,
∴∠1+∠2=∠1+∠DAC=45°.
故答案為:45°.


科目:初中數學 來源: 題型:
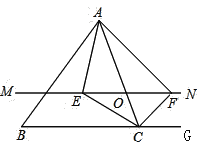
【題目】如圖,在![]() 中,點
中,點![]() 是
是![]() 邊上的一個動點,過點
邊上的一個動點,過點![]() 作直線
作直線![]() ,設
,設![]() 交
交![]() 的角平分線于點
的角平分線于點![]() ,交
,交![]() 的外角平分線于點
的外角平分線于點![]() .
.
(1)求證:![]() ;
;
(2)當點![]() 運動到何處時,四邊形
運動到何處時,四邊形![]() 是矩形?并證明你的結論.
是矩形?并證明你的結論.
(3)當點![]() 運動到何處,且
運動到何處,且![]() 滿足什么條件時,四邊形
滿足什么條件時,四邊形![]() 是正方形?并說明理由.
是正方形?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“龜兔首次賽跑”之后,輸了比賽的兔子沒有氣餒,總結反思后,和烏龜約定再賽一場.圖中的函數圖象刻畫了“龜兔再次賽跑”的故事(x表示烏龜從起點出發所行的時間,y1表示烏龜所行的路程,y2表示兔子所行的路程).有下列說法:

①“龜兔再次賽跑”的路程為1000米;
②兔子和烏龜同時從起點出發;
③烏龜在途中休息了10分鐘;
④兔子在途中750米處追上烏龜.
其中正確的說法是 .(把你認為正確說法的序號都填上)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C為線段AB上一點,點D為BC的中點,且AB=18cm,AC=4CD.
(1)圖中共有 條線段;
(2)求AC的長;
(3)若點E在直線AB上,且EA=2cm,求BE的長.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
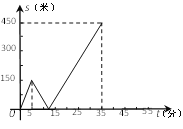
【題目】甲乙兩人勻速從同一地點到1500米處的圖書館看書,甲出發5分鐘后,乙以50米/分的速度沿同一路線行走.設甲乙兩人相距![]() (米),甲行走的時間為
(米),甲行走的時間為![]() (分),
(分),![]() 關于
關于![]() 的函數函數圖像的一部分如圖所示.
的函數函數圖像的一部分如圖所示.
(1)求甲行走的速度;
(2)在坐標系中,補畫![]() 關于
關于![]() 函數圖象的其余部分;
函數圖象的其余部分;
(3)問甲、乙兩人何時相距360米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:由絕對值的意義可知:當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .利用這一特性,可以幫助我們解含有絕對值的方程.比如:方程
.利用這一特性,可以幫助我們解含有絕對值的方程.比如:方程![]() ,
,
當![]() 時,原方程可化為
時,原方程可化為![]() ,解得
,解得![]() ;
;
當![]() 時,原方程可化為
時,原方程可化為![]() ,解得
,解得![]() .
.
所以原方程的解是![]() 或
或![]() .
.
(1)請補全題目中橫線上的結論.
(2)仿照上面的例題,解方程:![]() .
.
(3)若方程![]() 有解,則
有解,則![]() 應滿足的條件是 .
應滿足的條件是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一張三角形紙片ABC中,AB=10cm,BC=7cm,AC=6cm,沿過點B的直線折疊這個三角形,使頂點C落在邊AB上的點E處,折痕為BD.

(1)求△AED的周長.
(2)說明BD垂直平分EC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(背景知識)
數軸是初中數學的一個重要工具,利用數軸可以將數與形完美地結合.研究數軸我們發現了許多重要的規律:若數軸上點![]() 、點
、點![]() 表示的數分別為
表示的數分別為![]() 、
、![]() ,則
,則![]() 、
、![]() 兩點之間的距離
兩點之間的距離![]() ,線段
,線段![]() 的中點表示的數為
的中點表示的數為![]() .
.
(問題情境)
如圖,數軸上點![]() 表示的數為
表示的數為![]() ,點
,點![]() 表示的數為8,點
表示的數為8,點![]() 從點
從點![]() 出發,以每秒3個單位長度的速度沿數軸向右勻速運動,同時點
出發,以每秒3個單位長度的速度沿數軸向右勻速運動,同時點![]() 從點
從點![]() 出發,以每秒2個單位長度的速度向左勻速運動,設運動時間為
出發,以每秒2個單位長度的速度向左勻速運動,設運動時間為![]() 秒(
秒(![]() ).
).
(綜合運用)
(1)填空:
①![]() 、
、![]() 兩點之間的距離
兩點之間的距離![]() ________,線段
________,線段![]() 的中點表示的數為__________.
的中點表示的數為__________.
②用含![]() 的代數式表示:
的代數式表示:![]() 秒后,點
秒后,點![]() 表示的數為____________;點
表示的數為____________;點![]() 表示的數為___________.
表示的數為___________.
③當![]() _________時,
_________時,![]() 、
、![]() 兩點相遇,相遇點所表示的數為__________.
兩點相遇,相遇點所表示的數為__________.
(2)當![]() 為何值時,
為何值時,![]() .
.
(3)若點![]() 為
為![]() 的中點,點
的中點,點![]() 為
為![]() 的中點,點
的中點,點![]() 在運動過程中,線段
在運動過程中,線段![]() 的長度是否發生變化?若變化,請說明理由;若不變,請求出線段
的長度是否發生變化?若變化,請說明理由;若不變,請求出線段![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=x+5與x軸交于點A,直線y=﹣x+b與x軸交于點B(1,0),且這兩條直線交于點C.
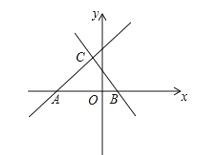
(1)求直線BC的解析式和點C的坐標;
(2)直接寫出關于x的不等式x+5>﹣x+b的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com