
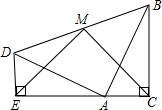
 兩個全等的含30°,60°角的三角板ADE和三角板ABC如圖所示放置,E,A,C三點在一條直線上,連接BD,取BD的中點M,連接ME,MC.試判斷線段ME和線段MC之間的關系,并說明理由.
兩個全等的含30°,60°角的三角板ADE和三角板ABC如圖所示放置,E,A,C三點在一條直線上,連接BD,取BD的中點M,連接ME,MC.試判斷線段ME和線段MC之間的關系,并說明理由. 分析 由全等三角形的性質可得到DA=AB,ED=AC,接下來可證明△DAB是等腰直角三角形依據直角三角形的性質可知AM=$\frac{1}{2}$BD=MD,然后可求得∠EDM=∠MAC=105°,接下來,可證明△MDE≌△MAC,依據全等三角形的性質可得到問題的答案.
解答 解:ME=MC.
連接MA.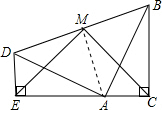
∵∠EAD=30°,∠BAC=60°,
∴∠DAB=90°,
∵△EDA≌△CAB,
∴DA=AB,ED=AC,
∴△DAB是等腰直角三角形.
又∵M為BD的中點,
∴∠MDA=∠MBA=45°,AM⊥BD(三線合一),
AM=$\frac{1}{2}$BD=MD,(直角三角形斜邊上的中線等于斜邊的一半)
∴∠EDM=∠MAC=105°,
在△MDE和△CAM中$\left\{\begin{array}{l}{ED=AC}\\{∠MDE=∠CAM}\\{MD=AM}\end{array}\right.$,
∴△MDE≌△MAC.
∴ME=MC.
點評 此題考查全等三角形的判定性質及等腰三角形性質,證得△MDE≌△MAC是解題的關鍵.


科目:初中數學 來源: 題型:填空題
 在如圖的八個頂點處分別標上1或-1,共有4個1和4個-1,將每個四邊形4個頂點處的數相乘,再將所得的所有的積相加.那么其和至多有2個不同的數值.
在如圖的八個頂點處分別標上1或-1,共有4個1和4個-1,將每個四邊形4個頂點處的數相乘,再將所得的所有的積相加.那么其和至多有2個不同的數值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
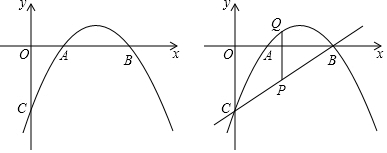
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
| 路程(千米) | 30 | 33 | 27 | 37 | 35 | 53 | 30 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com