
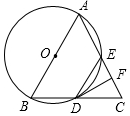
 如圖,AE是⊙O的直徑,B,D是⊙O上的點,AD與EB交于點C,連結AB和DE,過點E的直線與AC的延長線交于點F,且∠F=∠CED=∠AED.
如圖,AE是⊙O的直徑,B,D是⊙O上的點,AD與EB交于點C,連結AB和DE,過點E的直線與AC的延長線交于點F,且∠F=∠CED=∠AED.分析 (1)利用圓周角定理得到∠ADE=90°,則∠F+∠FED=90°,于是根據(jù)∠F=∠AED得到∠AEF=90°,然后根據(jù)切線的判定定理可得EF是⊙O切線;
(2)先證明△DCE∽△DEF,則利用相似比可計算出DE=6$\sqrt{2}$,再判斷△AEC為等腰三角形得到EA=EC,AD=CD=6,接著根據(jù)勾股定理得到AE=6$\sqrt{3}$,然后利用面積法計算出AB=4$\sqrt{6}$,最后利用勾股定理計算BE的長.
解答 (1)證明:∵AB為直徑,
∴∠ADE=90°,
∴∠F+∠FED=90°,
∵∠F=∠AED,
∴∠AED+∠FED=90°,即∠AEF=90°,
∴AE⊥EF,
∴EF是⊙O切線;
(2)解:∵∠CED=∠F,∠CDE=∠EDF,
∴△DCE∽△DEF,
∴$\frac{DC}{DE}$=$\frac{DE}{DF}$,即$\frac{6}{DE}$=$\frac{DE}{12}$,解得DE=6$\sqrt{2}$,
∵ED⊥AD,∠AED=∠CED,
∴△AEC為等腰三角形,
∴EA=EC,AD=CD=6,
在Rt△ADE中,AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{6}^{2}+(6\sqrt{2})^{2}}$=6$\sqrt{3}$,
∴EC=6$\sqrt{3}$,
∵$\frac{1}{2}$CE•AB=$\frac{1}{2}$DE•AC,
∴AB=$\frac{6\sqrt{2}×12}{6\sqrt{3}}$=4$\sqrt{6}$,
在Rt△ABE中,BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{(6\sqrt{3})^{2}-(4\sqrt{6})^{2}}$=2$\sqrt{3}$.
點評 本題考查了切線的判定:經過半徑的外端且垂直于這條半徑的直線是圓的切線.當已知條件中明確指出直線與圓有公共點時,常連接過該公共點的半徑,證明該半徑垂直于這條直線.熟練應用勾股定理和相似比計算線段的長是解決(2)小題的關鍵.


科目:初中數(shù)學 來源: 題型:解答題
 如圖,已知在△ABC中,AB=AC=13,BC=10,以AB為直徑作⊙O,交BC于D,交AC于E,DF⊥CE,垂足為F
如圖,已知在△ABC中,AB=AC=13,BC=10,以AB為直徑作⊙O,交BC于D,交AC于E,DF⊥CE,垂足為F查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,一農戶要建一個矩形雞舍,為了節(jié)省材料雞舍的一邊利用長為12米的墻,另外三邊用長為25米的建筑材料圍成,為方便進出,在垂直墻的一邊留下一個寬1米的門,所圍成矩形雞舍的長、寬分別是多少時,雞舍面積為80平方米?
如圖,一農戶要建一個矩形雞舍,為了節(jié)省材料雞舍的一邊利用長為12米的墻,另外三邊用長為25米的建筑材料圍成,為方便進出,在垂直墻的一邊留下一個寬1米的門,所圍成矩形雞舍的長、寬分別是多少時,雞舍面積為80平方米?查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,在長度為1個單位長度的小正方形組成的正方形網格中,點A、B、C在小正方形的頂點上.
如圖,在長度為1個單位長度的小正方形組成的正方形網格中,點A、B、C在小正方形的頂點上.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com