
【題目】如圖,P是矩形ABCD內部的一定點,M是AB邊上一動點,連接MP并延長與矩形ABCD的一邊交于點N,連接AN.已知AB=6cm,設A,M兩點間的距離為xcm,M,N兩點間的距離為y1cm,A,N兩點間的距離為y2cm.小欣根據學習函數的經驗,分別對函數y1,y2隨自變量x的變化而變化的規律進行了探究.下面是小欣的探究過程,請補充完整;
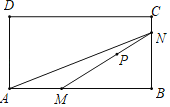
(1)按照如表中自變量x的值進行取點、畫圖、測量,分別得到了y1,y2與x的幾組對應值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.30 | 5.40 |
| 4.22 | 3.13 | 3.25 | 4.52 |
y2/cm | 6.30 | 6.34 | 6.43 | 6.69 | 5.75 | 4.81 | 3.98 |
(2)在同一平面直角坐標系xOy中,描出以補全后的表中各組對應值所對應的點(x,y1),并畫出函數y1的圖象;
(3)結合函數圖象,解決問題:當△AMN為等腰三角形時,AM的長度約為 cm.
【答案】(1) 4.80 ;(2)詳見解析;(3) 3.3或4.8或5.7.
【解析】
(1)根據實際取點、畫圖、測量,即可解決問題;
(2)利用描點法畫出函數圖象即可解決問題;
(3)通過圖象求出直線y=x與兩個函數圖象的交點坐標以及函數y1與y2的交點坐標即可解決問題.
(1)根據實際取點、畫圖、測量,可知當AM=2cm時,y1約為4.80cm.,
故答案為4.80.
(2)兩個函數圖象如圖所示:

(3)兩個函數與直線y=x的交點為A,B,函數y1與y2的交點為C,
觀察圖象可知:A(3.3,3.3),B(4.8,4.8),C(5.7,4).
∴△AMN為等腰三角形時,AM的值約為3.3或4.8或5.7.
故答案為3.3或4.8或5.7.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】![]() 嘗試探究
嘗試探究
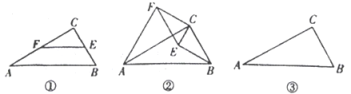
如圖-![]() ,在△ABC中,∠C=90°,∠A=30°,點E、F分別是BC、AC邊上的點,且EF//BC.
,在△ABC中,∠C=90°,∠A=30°,點E、F分別是BC、AC邊上的點,且EF//BC.
![]()
![]() 的值為 ;
的值為 ;![]() 直線
直線![]() 與直線
與直線![]() 的位置關系為 ;
的位置關系為 ;
![]() 類比延伸
類比延伸
如圖![]() ,若將圖
,若將圖![]() 中的
中的![]() 繞點
繞點![]() 順時針旋轉,連接
順時針旋轉,連接![]() ,則在旋轉的過程中,請判斷
,則在旋轉的過程中,請判斷![]() 的值及直線
的值及直線![]() 與直
與直![]() 線的位置關系,并說明理由;
線的位置關系,并說明理由;
![]() 拓展運用
拓展運用
若![]() ,在旋轉過程中,當
,在旋轉過程中,當![]() 三點在同一直線上時,請直接寫出此時線段
三點在同一直線上時,請直接寫出此時線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
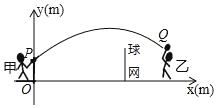
【題目】如圖是甲、乙兩人進行羽毛球練習賽時的一個瞬間,羽毛球飛行的高度y(m)與水平距離x(m)的路線為拋物線的一部分,如圖,甲在O點正上方1m的P處發出一球,已知點O與球網的水平距離為5m,球網的高度為1.55m.羽毛球沿水平方向運動4m時,達到羽毛球距離地面最大高度是![]() m.
m.
(1)求羽毛球經過的路線對應的函數關系式;
(2)通過計算判斷此球能否過網;
(3)若甲發球過網后,羽毛球飛行到離地面的高度為![]() m的Q處時,乙扣球成功求此時乙與球網的水平距離.
m的Q處時,乙扣球成功求此時乙與球網的水平距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
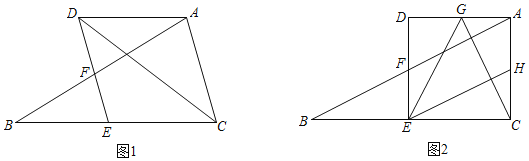
【題目】在△ABC中,過A作BC的平行線,交∠ACB的平分線于點D,點E是BC上一點,連接DE,交AB于點F,∠DEB+∠CAD=180°.
(1)如圖1,求證:四邊形ACED是菱形;
(2)如圖2,G是AD的中點,H是AC邊中點,連接CG、EG、EH,若∠ACB=90°,BC=2AC,在不添加任何輔助線的情況下,請直接寫出圖中與△CEH全等的三角形(不含△CEH本身).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】電影公司隨機收集了2000部電影的有關數據,經分類整理得到如表:
電影類型 | 第一類 | 第二類 | 第三類 | 第四類 | 第五類 | 第六類 |
電影部數 | 140 | 50 | 300 | 200 | 800 | 510 |
好評率 |
|
|
|
|
|
|
注:好評率是指一類電影中獲得好評的部數與該類電影的部數的比值.
![]() 如果電影公司從收集的電影中隨機選取1部,那么抽到的這部電影是獲得好評的第四類電影的概率是______;
如果電影公司從收集的電影中隨機選取1部,那么抽到的這部電影是獲得好評的第四類電影的概率是______;
![]() 電影公司為了增加投資回報,擬改變投資策略,這將導致不同類型電影的好評率發生變化
電影公司為了增加投資回報,擬改變投資策略,這將導致不同類型電影的好評率發生變化![]() 假設表格中只有兩類電影的好評率數據發生變化,那么哪類電影的好評率增加
假設表格中只有兩類電影的好評率數據發生變化,那么哪類電影的好評率增加![]() ,哪類電影的好評率減少
,哪類電影的好評率減少![]() ,可使改變投資策略后總的好評率達到最大?
,可使改變投資策略后總的好評率達到最大?
答:______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,正方形![]() 的邊長為
的邊長為![]() ,頂點
,頂點![]() 分別在
分別在![]() 軸、
軸、![]() 軸的正半軸,拋物線
軸的正半軸,拋物線![]() 經過
經過![]() 兩點,點
兩點,點![]() 為拋物線的頂點,連接
為拋物線的頂點,連接![]() .
.
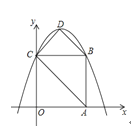
(1)求此拋物線的解析式;
(2)直接寫出四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過圓外一點P作⊙O的兩條切線,切點分別為A、B,連接AB,在AB、PB、PA上分別取一點D、E、F,使AD=BE,BD=AF,連接DE、DF、EF,則∠EDF等于( )
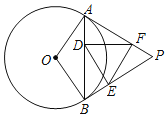
A.90°﹣∠PB.90°﹣![]() ∠PC.180°﹣∠PD.45°﹣
∠PC.180°﹣∠PD.45°﹣![]() ∠P
∠P
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某村計劃建造如圖所示的矩形蔬菜溫室,要求長與寬的比為2:1.在溫室內,沿前側內墻保留3m寬的空地,其它三側內墻各保留1m寬的通道.當矩形溫室的長與寬各為多少時,蔬菜種植區域的面積是288m2?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com