
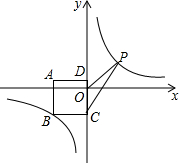
 如圖,正方形ABCD在平面直角坐標系中,且AD∥x軸,點A的坐標為(-4,1),點D的坐標為(0,1),點B,P都在反比例函數y=$\frac{k}{x}$的圖象上,且P時動點,連接OP,CP.
如圖,正方形ABCD在平面直角坐標系中,且AD∥x軸,點A的坐標為(-4,1),點D的坐標為(0,1),點B,P都在反比例函數y=$\frac{k}{x}$的圖象上,且P時動點,連接OP,CP.分析 (1)只需根據條件求出點B的坐標,然后運用待定系數法就可解決問題;
(2)易求出OC的長,然后只需根據條件求出點P的橫坐標,就可求出△OCP的面積,然后再求出正方形ABCD的面積,就可解決問題.
解答 解:(1)∵四邊形ABCD是正方形,A(-4,1),D(0,1),
∴OD=1,BC=DC=AD=4,
∴OC=3,
∴點B的坐標為(-4,-3).
∵點B在反比例函數y=$\frac{k}{x}$的圖象上,
∴k=-4×(-3)=12,
∴反比例函數的表達式為y=$\frac{12}{x}$;
(2)∵點P在反比例函數y=$\frac{12}{x}$的圖象上,點P的縱坐標為$\frac{9}{8}$,
∴點P的橫坐標為$\frac{32}{3}$,
∴S△OCP=$\frac{1}{2}$×3×$\frac{32}{3}$=16.
∵S正方形ABCD=16,
∴△OCP的面積與正方形ABCD的面積相等.
點評 本題主要考查正方形的性質、運用待定系數法求反比例函數的表達式、反比例函數圖象上點的坐標特征等知識,運用待定系數法是求函數解析式常用的方法,應熟練掌握.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案科目:初中數學 來源: 題型:解答題
 已知二次函數y=ax2+bx+c的圖象與坐標軸交于A、B、C三點,點A的坐標為(-1,0),點 C的坐標為 (0,3),對稱軸是x=1.
已知二次函數y=ax2+bx+c的圖象與坐標軸交于A、B、C三點,點A的坐標為(-1,0),點 C的坐標為 (0,3),對稱軸是x=1.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,AB=BC,∠ABC=100°,邊BA繞點B順時針旋轉m°,(0<m<180)得到線段BD,連接AD、DC,若△ADC為等腰三角形,則m所有可能的取值是130或100或160.
如圖,在△ABC中,AB=BC,∠ABC=100°,邊BA繞點B順時針旋轉m°,(0<m<180)得到線段BD,連接AD、DC,若△ADC為等腰三角形,則m所有可能的取值是130或100或160.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 47,45 | B. | 45,45 | C. | 40,45 | D. | 47,45 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | “抽出的圖形是中心對稱圖形”屬于必然事件 | |
| B. | “抽出的圖形是六邊形”屬于隨機事件 | |
| C. | 抽出的圖形為四邊形的概率是$\frac{2}{5}$ | |
| D. | 抽出的圖形為軸對稱圖形的概率是$\frac{3}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com