
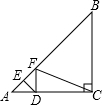
 如圖,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,點(diǎn)E為AB上一動點(diǎn),過點(diǎn)E作DE⊥AB交AC于D,將∠A沿 DE翻折,點(diǎn)A落在線段AB上的點(diǎn)F處,當(dāng)△BCF為等腰三角形時(shí),AE的長為$\frac{2-\sqrt{2}}{2}$或$\frac{1}{2}$.
如圖,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,點(diǎn)E為AB上一動點(diǎn),過點(diǎn)E作DE⊥AB交AC于D,將∠A沿 DE翻折,點(diǎn)A落在線段AB上的點(diǎn)F處,當(dāng)△BCF為等腰三角形時(shí),AE的長為$\frac{2-\sqrt{2}}{2}$或$\frac{1}{2}$. 分析 分兩種情形①BC=BF.②BF=CF分別求解即可.
解答 解:①當(dāng)BC=BF=$\sqrt{2}$時(shí),
在Rt△ABC中,∵∠ACB=90°,CA=BC=$\sqrt{2}$,
∴∠A=∠B=45°,AB=$\sqrt{2}$BC=2,
∵△DEF是由△DEA翻折得到,
∴AE=AF,△ADF是等腰直角三角形,
∵AF=AB-BF=2-$\sqrt{2}$,
∴AE=$\frac{2-\sqrt{2}}{2}$.
②當(dāng)FB=FC時(shí),易知AF=BF=CF=1,
∴AE=$\frac{1}{2}$AF=$\frac{1}{2}$.
故答案為$\frac{2-\sqrt{2}}{2}$或$\frac{1}{2}$.
點(diǎn)評 本題考查翻折變換、等腰直角三角形的性質(zhì)、勾股定理等知識,解題的關(guān)鍵是靈活運(yùn)用所學(xué)知識,學(xué)會用分類討論的思想思考問題,注意不能漏解.


 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $-\frac{5}{4}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,某水庫堤壩橫斷面迎水坡AB的斜面坡度是1:$\sqrt{3}$,堤壩高BC=50m,則迎水坡面AB的長度是( )
如圖,某水庫堤壩橫斷面迎水坡AB的斜面坡度是1:$\sqrt{3}$,堤壩高BC=50m,則迎水坡面AB的長度是( )| A. | 100m | B. | 120m | C. | 50$\sqrt{3}$m | D. | 100$\sqrt{3}$m |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,已知∠ACB=90°,AB=10,AC=8,DE垂直平分AC,垂足為E,DE交AB于D,連結(jié)CD,則CD的長為( )
如圖,已知∠ACB=90°,AB=10,AC=8,DE垂直平分AC,垂足為E,DE交AB于D,連結(jié)CD,則CD的長為( )| A. | 3 | B. | 4 | C. | 4.8 | D. | 5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -2a-a=-a | B. | -(-2)3=8 | C. | -5(a-b)=-5a+b | D. | (-2)4=8 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2ab2 | B. | 3ab | C. | -2a2b | D. | a2b2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
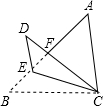 如圖,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.
如圖,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
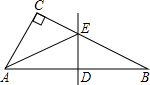 如圖,在△ABC中,∠C=90°,DE垂直平分斜邊AB,分別交AB,BC于點(diǎn)D,E,若∠CAE=∠B+36°,求∠AEB的度數(shù).
如圖,在△ABC中,∠C=90°,DE垂直平分斜邊AB,分別交AB,BC于點(diǎn)D,E,若∠CAE=∠B+36°,求∠AEB的度數(shù).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com