已知x1,x2是關于x的方程(x-2)(x-m)=(p-2)(p-m)的兩個實數根.
(1)求x1,x2的值;
(2)若p=3,設x1,x2是斜邊為5的直角三角形的兩直角邊的長,求m的值;
(3)在(2)的條件下,用得到的兩個全等的直角三角形可以拼成哪些凸四邊形?分別畫出示意圖,并在圖上標注出不重合的兩個對應定點之間的線段長.
【答案】
分析:(1)把所給式子進行重新整理,進行因式分解,進而求解.
(2)把p=3代入原方程,注意使用勾股定理.
(3)按相等的邊分別重合,分情況討論.
解答:解:(1)(x-2)(x-m)=(p-2)(p-m),
x
2-2x-mx+2m=p
2-2p-mp+2m,
∴x
2-(2+m)x-p
2+(2+m)p=0,
x
2-(2+m)x+p(2+m-p)=0,
(x-p)(x-2-m+p)=0,
∴x
1=p,x
2=m+2-p;
(2)∵p=3,
∴x
1=3,x
2=m-1,
而x
1,x
2是斜邊為5的直角三角形的兩直角邊的長
∴3
2+(m-1)
2=5
2,
故x
2=m-1=4,m=5;
(3)在(2)的條件下,用得到的兩個全等的直角三角形可以拼成矩形、平行四邊形等,
邊長分別為
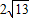
,
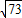
,5,4.8.
點評:注意隱含條件的運用,以及多種情況的分析.

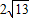 ,
,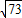 ,5,4.8.
,5,4.8.

 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案