
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .設
.設![]() 為最長邊.當
為最長邊.當![]() 時,
時,![]() 是直角三角形;當
是直角三角形;當![]() 時,利用代數式
時,利用代數式![]() 和
和![]() 的大小關系,探究
的大小關系,探究![]() 的形狀(按角分類).
的形狀(按角分類).
(1)當![]() 三邊分別為6、8、9時,
三邊分別為6、8、9時,![]() 為______三角形;當
為______三角形;當![]() 三邊分別為6、8、11時,
三邊分別為6、8、11時,![]() 為______三角形.
為______三角形.
(2)猜想,當![]() ______
______![]() 時,
時,![]() 為銳角三角形;當
為銳角三角形;當![]() ______
______![]() 時,
時,![]() 為鈍角三角形.
為鈍角三角形.
(3)判斷當![]() ,
,![]() 時,
時,![]() 的形狀,并求出對應的
的形狀,并求出對應的![]() 的取值范圍.
的取值范圍.
科目:初中數學 來源: 題型:
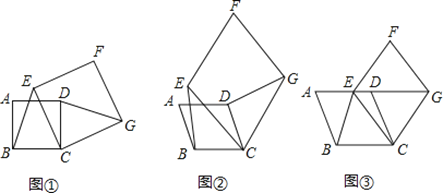
【題目】感知:如圖①,四邊形ABCD、CEFG均為正方形.易知BE=DG.
探究:如圖②,四邊形ABCD、CEFG均為菱形,且∠A=∠F.求證:BE=DG.
應用:如圖③,四邊形ABCD、CEFG均為菱形,點E在邊AD上,點G在AD的延長線上.若AE=3ED, ∠A=∠F,△EBC的面積為8,則菱形CEFG的面積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
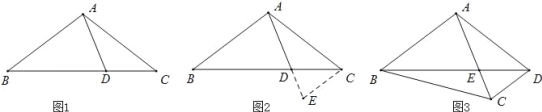
【題目】閱讀下面材料:小騰遇到這樣一個問題:如圖1,在△ABC中,點D在線段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的長.
小騰發現,過點C作CE∥AB,交AD的延長線于點E,通過構造△ACE,經過推理和計算能夠使問題得到解決(如圖 2).
請回答:∠ACE的度數為 ,AC的長為 .
參考小騰思考問題的方法,解決問題:
如圖 3,在四邊形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC與BD交于點E,AE=2,BE=2ED,求BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一空曠場地上設計一落地為矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m長的繩子一端固定在B點處,小狗在不能進入小屋內的條件下活動,其可以活動的區域面積為S(m2).①如圖1,若BC=4m,則S= m2.②如圖2,現考慮在(1)中的矩形ABCD小屋的右側以CD為邊拓展一正△CDE區域,使之變成落地為五邊形ABCED的小屋,其它條件不變則在BC的變化過程中,當S取得最小值時,邊BC的長為 m.

查看答案和解析>>
科目:初中數學 來源: 題型:
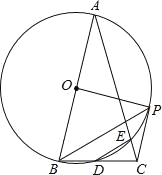
【題目】如圖,在△ABC中,AB=AC,∠A=30°,以AB為直徑的⊙O交BC于點D,交AC于點E,連結DE,過點B作BP平行于DE,交⊙O于點P,連結EP、CP、OP.
(1)BD=DC嗎?說明理由;
(2)求∠BOP的度數;
(3)求證:CP是⊙O的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的中線,
的中線,![]() 、
、![]() 分別是
分別是![]() 和
和![]() 延長線上的點,且
延長線上的點,且![]() ,連接
,連接![]() 、
、![]() ,下列說法:①
,下列說法:①![]() 和
和![]() 的面積相等,②
的面積相等,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中一定正確的答案有______________.(只填寫正確的序號)
,其中一定正確的答案有______________.(只填寫正確的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
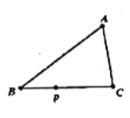
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 出發沿射線
出發沿射線![]() 以2
以2![]() 的速度運動,設運動時間為
的速度運動,設運動時間為![]()
![]() ,當
,當![]() 為等腰三角形時,
為等腰三角形時,![]() 的值為( )
的值為( )
A.![]() 或
或![]() B.
B.![]() 或12或4C.
或12或4C.![]() 或
或![]() 或12D.
或12D.![]() 或12或4
或12或4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的袋中裝有5個黃球、13個黑球和22個紅球,它們除顏色外都相同。
(1)求從袋中摸出一個球是黃球的概率;
(2)現從袋中取出若干個黑球,并放入相同數量的黃球,攪拌均勻后,使從袋中摸出一個球是黃球的概率不小于![]() ,問至少取出了多少個黑球?
,問至少取出了多少個黑球?
查看答案和解析>>
科目:初中數學 來源: 題型:
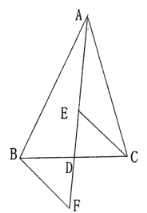
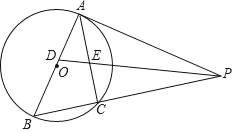
【題目】如圖,以AB為直徑的⊙O外接于△ABC,過A點的切線AP與BC的延長線交于點P,∠APB的平分線分別交AB,AC于點D,E,其中AE,BD(AE<BD)的長是一元二次方程x2﹣5x+6=0的兩個實數根.
(1)求證:PABD=PBAE;
(2)在線段BC上是否存在一點M,使得四邊形ADME是菱形?若存在,請給予證明,并求其面積;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com