【題目】在一空曠場地上設計一落地為矩形ABCD的小屋，AB+BC＝10m．拴住小狗的10m長的繩子一端固定在B點處，小狗在不能進入小屋內的條件下活動，其可以活動的區域面積為S（m2）．①如圖1，若BC＝4m，則S＝ m2．②如圖2，現考慮在（1）中的矩形ABCD小屋的右側以CD為邊拓展一正△CDE區域，使之變成落地為五邊形ABCED的小屋，其它條件不變則在BC的變化過程中，當S取得最小值時，邊BC的長為 m．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中，矩形ABCD的邊AB:BC＝3:2，點A（3，0），B（0，6）分別在x軸，y軸上，反比例函數
(x＞0)的圖像經過點D，則
值為（ ）
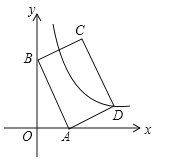
A. ﹣14 B. 14 C. 7 D. ﹣7
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝AC，點D，E，F分別在邊BC，AC，AB上，且BD＝CE，DC＝BF，連結DE，EF，DF，∠1＝60°
（1）求證：△BDF≌△CED．
（2）判斷△ABC的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
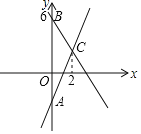
【題目】如圖，一次函數y1＝2x﹣2的圖象與y軸交于點A，一次函數y2的圖象與y軸交于點B（0，6），點C為兩函數圖象交點，且點C的橫坐標為2．
（1）求一次函數y2的函數解析式；
（2）求△ABC的面積；
（3）問：在坐標軸上，是否存在一點P，使得S△ACP＝2S△ABC，請直接寫出點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖A村和B村在一條大河CD的同側，它們到河岸的距離AC、BD分別為1千米和4千米，又知道CD的長為4千米.
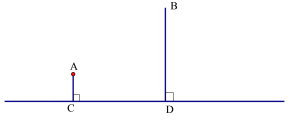
（1）現要在河岸CD上建一水廠向兩村輸送自來水.有兩種方案備選.
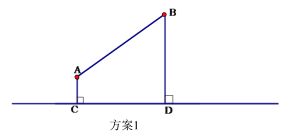
方案1：水廠建在C點，修自來水管道到A村，再到B 村（即AC+AB）.（如圖）
方案2：作A點關于直線CD的對稱點
，連接
交CD 于M點，水廠建在M點處，分別向兩村修管道AM和BM. （即AM+BM） （如圖）
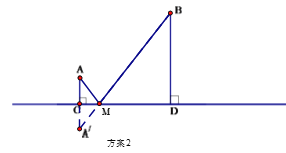
從節約建設資金方面考慮，將選擇管道總長度較短的方案進行施工.請利用已有條件分別進行計算，判斷哪種方案更合適.
（2）有一艘快艇Q從這條河中駛過，當快艇Q與CD中點G相距多遠時，△ABQ為等腰三角形？直接寫出答案，不要說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在
中，
，
，
.設
為最長邊.當
時，是直角三角形；當
時，利用代數式
和
的大小關系，探究的形狀（按角分類）．
（1）當三邊分別為6、8、9時，為______三角形；當三邊分別為6、8、11時，為______三角形．
（2）猜想，當______時，為銳角三角形；當______時，為鈍角三角形．
（3）判斷當
，
時，的形狀，并求出對應的的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，BD是⊙O的弦，延長BD到點C，使DC=BD，連結AC交⊙O于點F．
（1）AB與AC的大小有什么關系？請說明理由；
（2）若AB=8，∠BAC=45°，求：圖中陰影部分的面積．
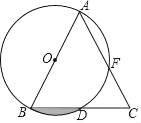
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，∠A=30°，點O是邊AB上一點，以點O為圓心，以OB為半徑作圓，⊙O恰好與AC相切于點D，連接BD．若BD平分∠ABC，AD=2
，則線段CD的長是（ ）
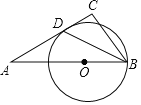
A. 2 B. C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
