
【題目】已知如圖,拋物線![]() 經過點
經過點![]() 、
、![]() .
.
![]() 求
求![]() 、
、![]() 的值;
的值;
![]() 如圖,點
如圖,點![]() 與點
與點![]() 關于點
關于點![]() 對稱,過點
對稱,過點![]() 的直線交
的直線交![]() 軸于點
軸于點![]() ,交拋物線于另一點
,交拋物線于另一點![]() .若
.若![]() ,求
,求![]() 的值;
的值;
![]() 如圖,在
如圖,在![]() 的條件下,點
的條件下,點![]() 是
是![]() 軸上一點,連
軸上一點,連![]() 、
、![]() 分別交拋物線于點
分別交拋物線于點![]() 、
、![]() ,探究
,探究![]() 與
與![]() 的位置關系,并說明理由.
的位置關系,并說明理由.

【答案】(1)b=-2,c=-3;(2)1;(3)見解析.
【解析】
(1)利用待定系數法即可解決問題.
(2)取點Q(1,4),P(0,1),如圖1中,作QR⊥y軸于R,連接PQ,則RQ=OP=1,PR=OC=OB=3,由△POR≌△BPO≌△CAO,推出BQ與y軸的交點是N,與拋物線的交點是M,利用方程組即可解決問題.
(3)結論:EF∥BM或EF與BM重合.設P(0,m),求出直線PM、PB,再利用方程組求出點E、F坐標,求出直線EF的解析式即可解決問題.
解:![]() ∵拋物線
∵拋物線![]() 經過點
經過點![]() 、
、![]() ,
,
∴有方程組![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() .
.
![]() ∵拋物線解析式為
∵拋物線解析式為![]() ,
,

∴點![]() 坐標
坐標![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵點![]() 與點
與點![]() 關于點
關于點![]() 對稱
對稱
∴![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]() ,
,
取點![]() ,
,![]() ,如圖
,如圖![]() 中,作
中,作![]() 軸于
軸于![]() ,連接
,連接![]() ,則
,則![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴由此![]() 與
與![]() 軸的交點是
軸的交點是![]() ,與拋物線的交點是
,與拋物線的交點是![]() ,
,
∵![]() ,
,![]() ,設直線
,設直線![]() 為
為![]() ,則
,則![]() ,解得
,解得![]() ,
,
∴直線![]() 的解析式為
的解析式為![]() ,
,
∴![]() ,
,
由![]() 解得
解得![]() 或
或![]() ,
,
∵![]() ,∴
,∴![]() ,
,
作![]() 軸于
軸于![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∴![]() .
.
![]() 結論:
結論:![]() 或
或![]() 與
與![]() 重合.
重合.
理由:設![]() ,
,
∵![]() ,
,![]() ,
,
∴可得直線![]() 的解析式為
的解析式為![]() ,直線
,直線![]() 的解析式為
的解析式為![]() ,
,
由 消去
消去![]() 得
得![]() ,
,![]() ,
,
∴![]() 或
或![]() ,
,![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,

∴方程組的解為![]() 或
或 ,
,
∴![]() ,
,
由 解得
解得![]() 或
或 ,
,
∴![]() ,
,
設直線![]() 解析式為
解析式為![]() ,
,
則 ,
,
∴![]() ,
,
∴![]() ,
,
∴直線![]() 的解析式為
的解析式為![]() ,
,
∵直線![]() 的解析式為
的解析式為![]() ,
,
∴![]() 時,
時,![]() ,
,![]() 時,直線
時,直線![]() 與
與![]() 重合.
重合.


 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:
【題目】探究題:如圖,AB⊥BC,射線CM⊥BC,且BC=5cm,AB=1cm,點P是線段BC(不與點B、C重合)上的動點,過點P作DP⊥AP交射線CM于點D,連結AD.

(1)如圖1,若BP=4cm,則CD= ;
(2)如圖2,若DP平分∠ADC,試猜測PB和PC的數量關系,并說明理由;
(3)若△PDC是等腰三角形,則CD= cm.(請直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某茶葉公司經銷一種茶葉,每千克成本為![]() 元,市場調查發現在一段時間內,銷量
元,市場調查發現在一段時間內,銷量![]() (千克)隨銷售單價
(千克)隨銷售單價![]() (元/千克)的變化而變化,具有關系為:
(元/千克)的變化而變化,具有關系為:![]() ,物價部門規定每千克的利潤不得超過
,物價部門規定每千克的利潤不得超過![]() 元.設這種茶葉在這段時間內的銷售利潤
元.設這種茶葉在這段時間內的銷售利潤![]() (元),解答下列問題:
(元),解答下列問題:
![]() 求
求![]() 與
與![]() 的關系式;
的關系式;
![]() 當
當![]() 取何值時,
取何值時,![]() 的值最大?并求出最大值;
的值最大?并求出最大值;
![]() 當銷售利潤
當銷售利潤![]() 的值最大時,銷售額也是最大嗎?判斷并說明理由.
的值最大時,銷售額也是最大嗎?判斷并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一個關于![]() 的代數式
的代數式![]() ,若存在一個系數為正數關于
,若存在一個系數為正數關于![]() 的單項式
的單項式![]() ,使
,使![]() 的結果是所有系數均為整數的整式,則稱單項式
的結果是所有系數均為整數的整式,則稱單項式![]() 為代數式
為代數式![]() 的“整系單項式” ,例如:
的“整系單項式” ,例如:
當![]() 時,由于
時,由于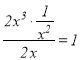 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于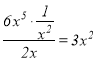 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于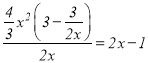 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于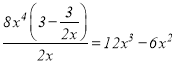 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
顯然,當代數式![]() 存在整系單項式
存在整系單項式![]() 時,
時,![]() 有無數個,現把次數最低,系數最小的整系單項式
有無數個,現把次數最低,系數最小的整系單項式![]() 記為
記為![]() ,例如:
,例如:![]() .
.
閱讀以上材料并解決下列問題:
⑴.判斷:當![]() 時,
時,![]()
![]() 的整系單項式(填“是”或“不是”);
的整系單項式(填“是”或“不是”);
⑵.當![]() 時,
時,![]() = ;
= ;
⑶.解方程: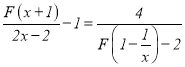 .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AD⊥BC于點D,則下列四個結論中:
①線段AD上任意一點到點B的距離與到點C的距離相等;
②線段AD上任意一點到AB的距離與到AC的距離相等;
③若點Q是線段AD的三等分點 ,則△ACQ的面積是△ABC面積的![]() ;
;
④若![]() ,則
,則![]() ;
;
正確結論的序號是( )

A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一艘在南北航線上的測量船,于A點處測得海島B在點A的南偏東30°方向,繼續向南航行30海里到達C點時,測得海島B在C點的北偏東15°方向,那么海島B離此航線的最近距離是( )(結果保留小數點后兩位)(參考數據:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
A. 4.64海里 B. 5.49海里 C. 6.12海里 D. 6.21海里
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com